Happy Halloween! To celebrate the holiday, I’m turning my attention to an animal long associated with the holiday: bats! No, not the blood-sucking bats of vampire lore: This post focuses on a species called the greater horseshoe bat. Their dietary preference is insects.

Two greater horseshoe bats.

Bats are far from the cutest or cuddliest of animals but make no mistake—they play an important role in our environment. They are proficient pollinators and skillful seed spreaders. They are also one of the best natural insect control methods around, reducing the pesticides farmers need where there are active colonies. A single bat consumes up to 8,000 insects each night, so it’s no surprise that ecologists and biologists want to study these creatures. But mathematicians? Yes, them too!

The greater horseshoe bat is one of the UK’s largest bats, with a wingspan of up to 40 cm (almost 16 inches). It can live up to 30 years and gets its name from its horseshoe-shaped nose. Sadly, the population of greater horseshoe bats is estimated to have declined by 90% in the last century. Finding and protecting their roosts is important, and studying the behavior of the colonies is an important step.

Combining Biology and Mathematics in Research

Bats are susceptible to human activity, such as noise and light pollution, and locating their roosts is a necessary step for protecting the population. Understanding the movements of bats dispersing from and returning to their roost would help predict the location of the roost. Determining the extent of their foraging habitat is also important for bat conservation.

A team of researchers studied how bats travel back from their nightly foraging in a pattern that maximizes their hunting time while minimizing their exposure to predators, such as birds of prey. The team included Dr. Fiona Mathews, a professor of environmental biology at the University of Sussex, and Dr. Thomas Wooley, senior lecturer at the applied mathematics department at Cardiff University. Pairing mathematics with biology enabled the team to use math to analyze the bats’ behavior. Their research was published in the Bulletin of Mathematical Biology.

The Guardian reported the team “developed a mathematical model using “trajectory data” that tracked the flight of greater horseshoe bats in Devon to pinpoint how the creatures engage with the nocturnal environment.”

In a video describing the work, Professor Mathews spoke about how applying math to study the bats changed the approach. “So normally, I would follow bats around in the landscape and then try to deduce what they are doing afterward. How are they behaving? Whereas working with Thomas, we’ve kind of done this the opposite way round, where he comes up with some theoretical principles of saying, ‘I think the bats might behave like this.’”

For this study, the team trapped several bats in a harp trap, fitted them with tiny radio receivers with bat-safe glue, and then released them back into the wild. Radio tracking data was collected for 14 nights, from when the bats left the roost to when they returned.

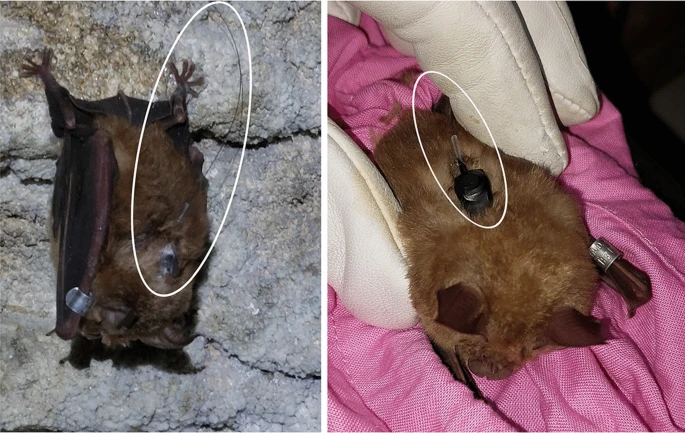
Greater horseshoe bats with radio transmitters glued to their backs. The radio transmitters have very thin antennae and are highlighted in white. Image credit: Professor Fiona Mathews.

BATLAB, um, I mean MATLAB

The recordings provided a few hundred trajectories of the bats’ locations throughout their flights. Processing the data was key to understanding their travels.

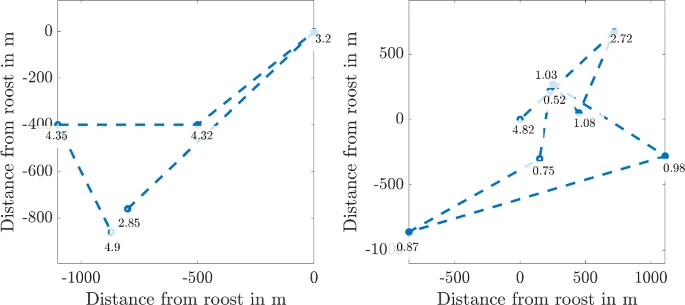
The locations of the same bat over two nights during the survey. The roost has been normalized to be at the origin in each case. The circles represent detections, and the numbers next to them represent the time in hours after sunset when the bat was detected at the given location. Image credit: Wooley et. Al.

To better understand the bats’ location, the team turned to mathematics using mean square displacement. As Dr. Wooley described in a video, “The reason we just take the displacement and square is to reduce the two-dimensional information […]. Bats fly in three dimensions, but unfortunately, we can’t say how high they are. So, we have to flatten it first to two dimensions. Where are you on a map? Then we flatten it to one dimension of just how far away [you are] from your roosts.”

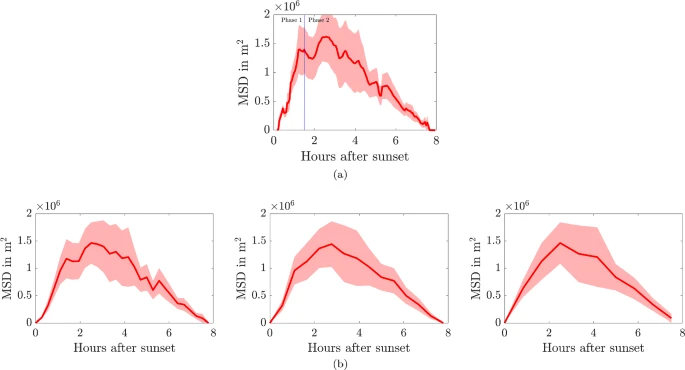
a The mean-squared distance (MSD) for all radio-tracked bats interpolated at Δt=200s. b The MSD for all radio-tracked bats interpolated at Δt=1000, 2000, and 3000 s, from left to right, respectively. The red line is the MSD trajectory, and the ribbon represents the mean ±standard error of the squared displacement trajectory data. Image credit: Wooley et. Al.

Using MATLAB to analyze their results, the team found that the bats furthest out started returning first. The MATLAB code for the calculations and graphics is available in this GitHub repository.

The team described the motion in the paper, “We term this form of motion ‘leap frogging’ because it mirrors the idea that bats on the periphery will choose to fly towards the roost until they are no longer the furthest bat away from the roost. Once the convecting bat is no longer the furthest out from the roost it stops convecting and returns to moving randomly. The new bat that is furthest out starts to convect towards the roost and the process begins again. Note that the furthest out bat becomes the edge of the domain and no randomly moving bat is able to move past it. Over time this form of motion will cause the bat population to tend towards the roost.”

The team postulates that the bat that is furthest out has three possible motivations to leapfrog back into the midst of other bats: A) Lessen its exposure to predators, B) They have the furthest to travel, and moving closer allows more time for foraging, and C) “[…] if the rest of the bat population has found suitable foraging areas closer to the roost the furthest out bat is wasting energy by flying further.”

But how do the bats know they are the furthest away? They only hear other bats, and the corresponding echolocation clicks from one direction. When they are among their fellow bats, the clicks come from multiple directions.

No matter the motivation, we now know that these bats act like frogs in two ways: They love to munch on insects and have a propensity to leapfrog their way home.

To read the full research paper, see DOI: 10.1007/s11538-023-01233-5

If you want more quirky animal trivia for Halloween, check out this post on “Pumpkin” toadlets.

Pumpkin toadlet. Image credit: Luiz F. Ribeiro.