bio_img_japan-community

MATLAB ユーザーコミュニティー

MATLAB & Simulink ユーザーコミュニティー向け日本語ブログ

MATLAB MCP Core Server を活用した最適化エージェントの作り方

作者 Michio Inoue,

47 次查看（过去 30 天）  |   个赞   |   0 个评论

※この投稿は 2026 年 1 月 26 日に Artificial Intelligence へ 投稿されたものの抄訳です。

—
Co-author: Tom Couture

Tom Couture は最適化（Optimization）のプロダクトマネージャーです。このブログ記事では、彼が私と一緒に行った、新しい MATLAB MCP Core Server を使った最適化エージェントを構築する方法を紹介します。

Tom のような方であれば、MATLAB で最適化問題を設定するのに、目的関数や制約を定義し、ソルバーを選び、オプションを微調整するなど、何時間も費やした経験があるかもしれません。では、これが実現できたらどうでしょうか——それらすべてを代わりにやってくれる AI エージェントと会話しつつ、最適化自体は手元の MATLAB で実行できるとしたら？ まるで「ポケットの中の小さな Tom」のように。

そこで登場するのが、強力な Optimization Toolbox™ と組み合わせて利用できる MATLAB MCP Core Server です。この記事では、実際のエンジニアリング課題を解ける最適化エージェントを作成する方法を紹介します。シンプルな制約付き最適化から、サロゲートモデルを使った計算コストの高い CFD ベースの設計最適化まで取り扱います。

エージェントが最初に行うべきこと：ツールボックスの確認

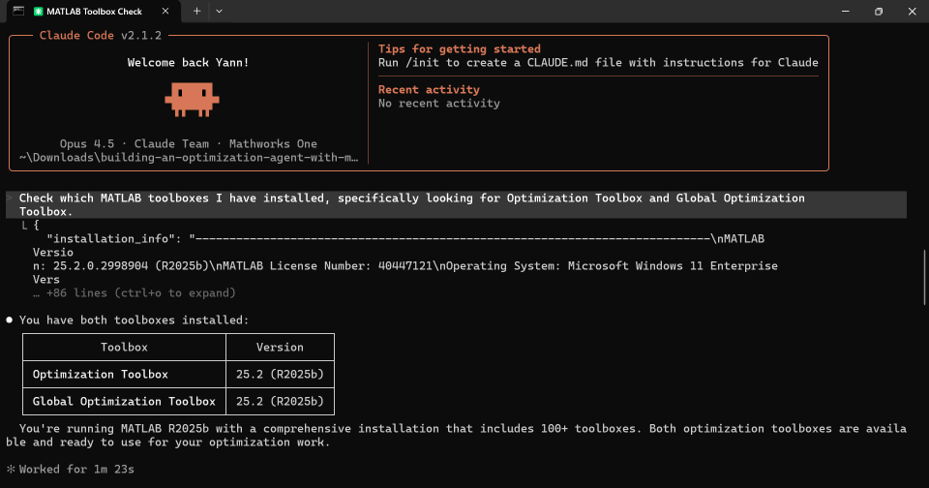
私が MATLAB MCP Core Server のデモで最初に紹介する機能のひとつが、 detect_matlab_toolboxes ツールです。エージェントが最適化のコードを書き始める前に、必要なツールボックスがインストールされているかを確認する必要があります。

AI アシスタント（Claude Desktop®、GitHub Copilot®、または任意の MCP 対応クライアント）へのプロンプトの例は次のとおりです：

“Check which MATLAB toolboxes I have installed, specifically looking for Optimization Toolbox and Global Optimization Toolbox.”

日本語訳：インストールされている MATLAB のツールボックスを確認してください。特に Optimization Toolbox と Global Optimization Toolbox を探してください。

エージェントは detect_matlab_toolboxes ツールを呼び出し、次のような結果を返します：

Optimization Toolbox – Version 25.2 (R2025b) ✓
Global Optimization Toolbox – Version 25.2 (R2025b) ✓

これは非常に重要です。使用できるソルバーは、あなたが保有しているライセンスに完全に依存しているためです。Optimization Toolbox がない？ その場合、エージェントは fminsearch に切り替える必要があることを判断します。Global Optimization Toolbox がある？素晴らしい！ これにより、計算コストの高いシミュレーションには surrogateopt を利用できます。

 

例 1：構造梁の設計最適化

まず、古典的なエンジニアリング最適化問題をデモしましょう。応力とたわみの制約を満たしつつ、片持ち梁の重量を最小化する設計問題です。

問題設定

矩形断面の梁について、その重量を最小化することを目指します。ただし、以下の条件を満たす必要があります：

  • 最大応力の制約（降伏応力を超えてはならない）
  • 最大たわみの制約（許容たわみを超えてはならない）
  • 幅と高さの上下限
Claude Code に与えたプロンプトは次のとおりです：

“I need to optimize a cantilever beam design. The beam has length L=5m, carries a tip load P=10kN, made of steel with E=200 GPa and yield stress=250 MPa. I want to minimize the cross-sectional area (width × height) while keeping tip deflection under 10mm and max stress under the yield stress. Width should be between 50-200mm, height between 100-500mm. Please set this up and solve it using MATLAB.”

日本語訳：片持ち梁の設計を最適化したいです。梁の長さ L = 5 m、先端荷重 P = 10 kN、材料は E = 200 GPa、降伏応力は 250 MPa の鋼です。断面積（幅 × 高さ）を最小化したいのですが、先端たわみを 10 mm 以下、最大応力を降伏応力以下に保つ必要があります。幅は 50–200 mm、高さは 100–500 mm の範囲にしてください。これを MATLAB を使って設定し、解いてください。

エージェントは次のコードを生成して実行しました：

% Beam optimization problem
L = 5; % Length [m]
P = 10000; % Tip load [N]
E = 200e9; % Young’s modulus [Pa]
sigma_yield = 250e6; % Yield stress [Pa]
delta_max = 0.010; % Max deflection [m]
% Objective: minimize cross-sectional area
objective = @(x) x(1) * x(2); % width * height
% Nonlinear constraints
nonlcon = @(x) beamConstraints(x, L, P, E, sigma_yield, delta_max);
% Bounds: [width_min, height_min] to [width_max, height_max]
lb = [0.05, 0.10]; % [m]
ub = [0.20, 0.50]; % [m]
% Initial guess
x0 = [0.10, 0.25];
% Solve
options = optimoptions(‘fmincon’, ‘Display’, ‘iter’, ‘Algorithm’, ‘sqp’);
[x_opt, fval, exitflag] = fmincon(objective, x0, [], [], [], [], lb, ub, nonlcon, options);
fprintf(‘Optimal width: %.1f mm\n’, x_opt(1)*1000);
fprintf(‘Optimal height: %.1f mm\n’, x_opt(2)*1000);
fprintf(‘Optimal area: %.2f cm²\n’, fval*1e4);
制約は以下の通り。
function [c, ceq] = beamConstraints(x, L, P, E, sigma_yield, delta_max)
b = x(1); % width
h = x(2); % height
I = b * h^3 / 12; % Second moment of area
sigma = P * L * (h/2) / I; % Max bending stress
delta = P * L^3 / (3 * E * I); % Tip deflection
c(1) = sigma – sigma_yield; % Stress constraint
c(2) = delta – delta_max; % Deflection constraint
ceq = [];
end
結果はどうだったでしょうか？
幅 80.2 mm、高さ 189.4 mm の最適な梁が得られ、どちらの制約も境界でちょうど満たしています。これは、適切に定式化された最適化問題ならまさに期待される挙動です。

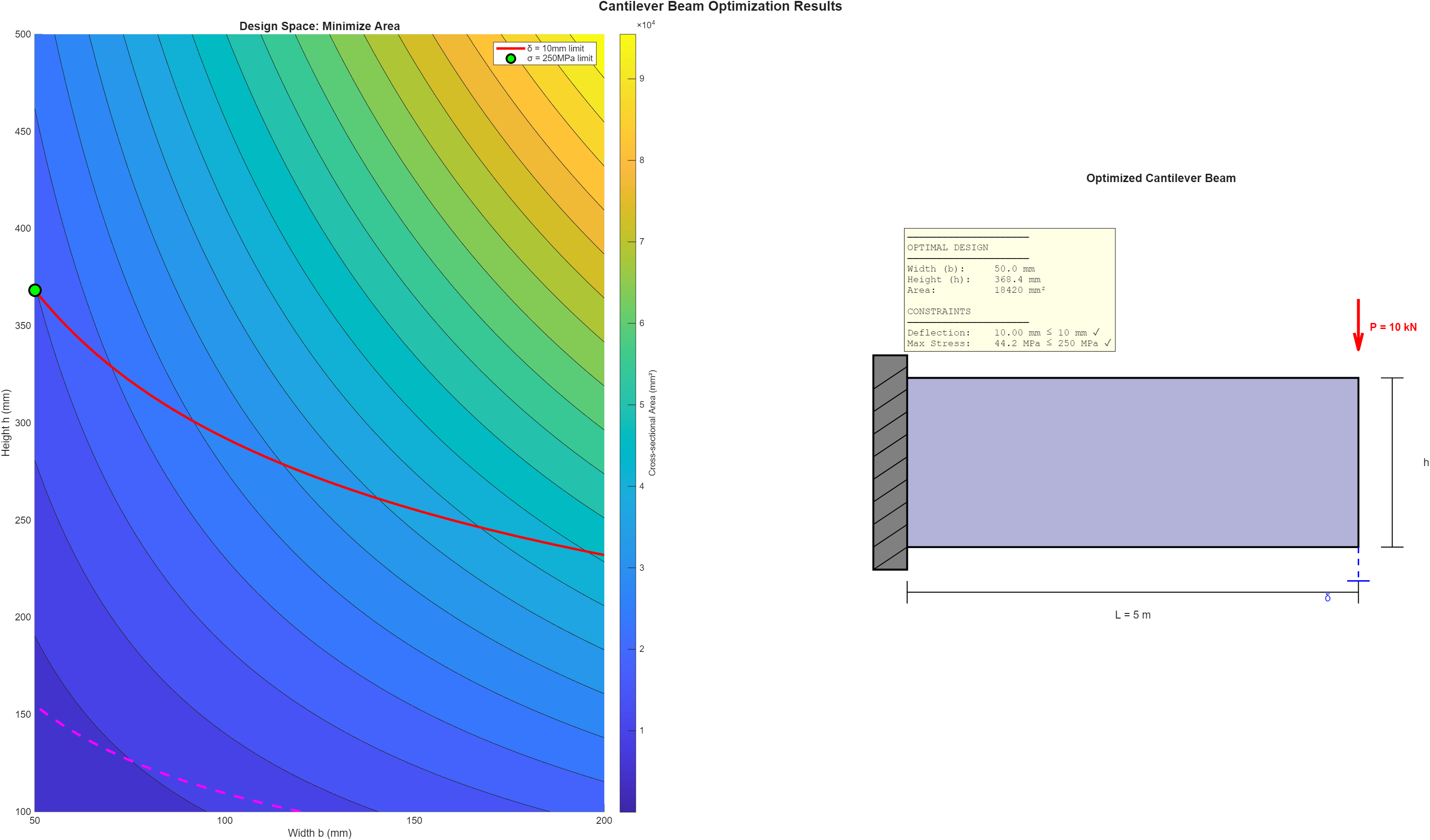
なぜこの問題に対して fmincon ソルバーを使用したのか、その理由の一部は、私と Claude とのやり取りを見ると確認できます：

また、リポジトリでは問題ベースアプローチのための「スキル」も公開しています：

例 2：応答曲面を用いた CFD ベースの最適化

では、ここからが面白いところです。MATLAB での最適化の中でも特に気に入っている応用例のひとつは、CFD のように計算コストの高いシミュレーションに対して、最適な設計パラメータを求める場合です。

蓋駆動キャビティ流れ問題

蓋駆動キャビティ流れは CFD における「Hello World」とも言える問題です。上部の壁（“蓋・lid”）が一定速度で動く正方形キャビティで、ナビエ–ストークス方程式を解いて流れ場を求めます。このデモでは、日本の同僚である Michio が MATLAB のみで実装したコードを使用します。コードは GitHub にあります：2D Lid-Driven Cavity Flow Solver

エージェントに対して与えた質問は次のとおりです：
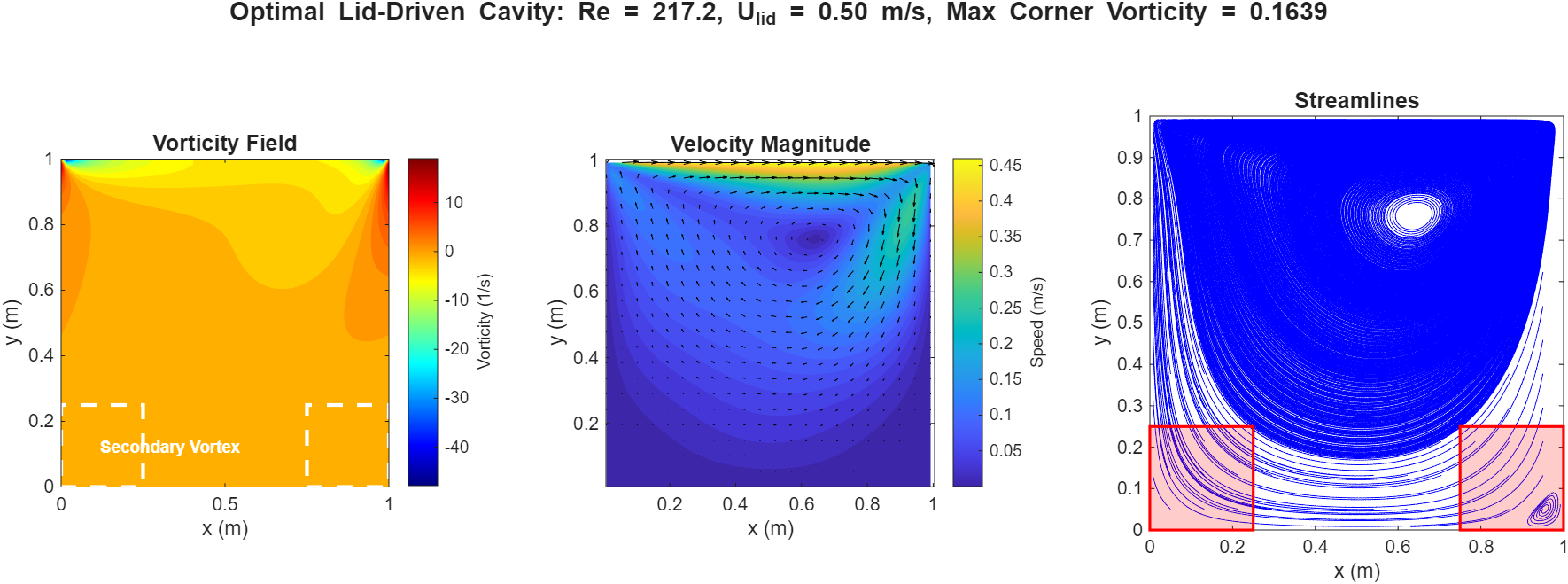
“I have a CFD solver in the folder 2D-Lid-Driven-Cavity-Flow-Incompressible-Navier-Stokes-Solver. I want to optimize the lid velocity and Reynolds number to minimize the maximum vorticity in the secondary corner vortex of a lid-driven cavity flow. Reynolds number should be between 100 and 1000, and lid velocity between 0.5 and 2.0 m/s.”

日本語訳：フォルダ 2D-Lid-Driven-Cavity-Flow-Incompressible-Navier-Stokes-Solver に CFD ソルバーがあります。蓋駆動キャビティ流れの二次コーナー渦における最大渦度を最小化するために、蓋速度とレイノルズ数を最適化したいです。レイノルズ数は 100〜1000、蓋速度は 0.5〜2.0 m/s の範囲にしてください。

なぜサロゲート最適化なのか？

CFD の目的関数に対して fmincon を実行したことがある方なら、その非効率さをご存じでしょう。関数評価 1 回に 30 秒かかり、勾配ベースの手法では数百回の評価が必要になることもあります。Global Optimization Toolbox の surrogateopt は、まさにこのような状況のために設計されています。
What’s New
Why It Matters
高価な関数のサロゲート（応答曲面）を構築する
実際の CFD シミュレーションの回数を減らせる
放射基底関数（RBF）補間を使用
複雑な応答面でも正確に近似できる
グローバル探索が可能
局所解にハマらない
並列評価をサポート
CPU コアを最大活用できる
エージェントが生成したコードは次のとおりです：
% Define bounds
lb = [100, 0.5]; % [Re_min, V_min]
ub = [1000, 2.0]; % [Re_max, V_max]
% Set up surrogate optimization
options = optimoptions(‘surrogateopt’, …
‘Display’, ‘iter’, …
‘PlotFcn’, ‘surrogateoptplot’, …
‘MaxFunctionEvaluations’, 50, …
‘MinSurrogatePoints’, 20);
% Run optimization
[x_opt, fval, exitflag, output] = surrogateopt(@cavityObjective, lb, ub, options);
fprintf(‘Optimal Reynolds number: %.0f\n’, x_opt(1));
fprintf(‘Optimal lid velocity: %.2f m/s\n’, x_opt(2));
fprintf(‘Minimum corner vorticity: %.4f\n’, fval);
目的関数は以下の通り
function obj = cavityObjective(x)
Re = x(1);
V_lid = x(2);
% Run CFD simulation (using 2D-Lid-Driven-Cavity solver)
[u, v] = runCavitySimulation(Re, V_lid);
% Calculate vorticity in corner region
[vorticity] = calculateVorticity(u, v);
% Extract max vorticity in secondary vortex region
cornerRegion = vorticity(1:20, 1:20);
obj = max(abs(cornerRegion(:)));
end
surrogateopt のすばらしさは、探索を進めながら応答曲面を構築していく点にあります。わずか 20 回の関数評価（約 5 分）で最適な操作点を見つけました。これは、グリッドサーチなら数時間かかったであろう処理です。

次は？

MATLAB MCP Core Server と Optimization Toolbox の組み合わせは、エンジニアリング最適化の新しい形を切り開きます。

ドキュメント、コードエディタ、コマンドウィンドウを行き来するのではなく、AI と会話しながら次のようなことができるようになります：

  • 利用可能なソルバーを知るためにツールボックスをチェックする
  • 自然言語で記述した内容から問題を定式化する
  • ローカルの MATLAB でコードを書いて実行する
  • エラーが出てもコピー＆ペーストなしで自動的に反復して改善する

自分でも試してみたい場合は、MATLAB MCP Core Server のリポジトリにアクセスし、セットアップ手順に従ってください。サーバーは 5 つのコアツールを提供していますが、Optimization Toolbox に含まれる 100 以上の関数と組み合わせれば、可能性は無限大です。

最適化を楽しんでください！

See Also

Special thanks to Michio Inoue for the cavity flow solver.

|
类别: 
Artificial Intelligence,
機能と使い方,
生成AI
  • print

评论

要发表评论，请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。