Playing with the R2022b MATLAB Apple Silicon beta for M1/M2 Mac
Update 22nd June 2023: An updated blog post about MATLAB on Apple Silicon can be found at https://blogs.mathworks.com/matlab/2023/06/22/native-apple-silicon-support-in-the-matlab-simulink-r2023b-pre-release
Since the release of the first MATLAB beta for Apple Silicon, MathWorkers have been toiling away to bring more of the MATLAB experience to this platform and I'm very happy to be able to announce that we have something new for you - MATLAB R2022b Native Apple Silicon Platform Open Beta. This beta will be available until June 30, 2023.
It's faster, more stable and with a bunch of toolboxes alongside MATLAB itself. Your feedback was crucial to getting us here so we encourage you to try out the new release and let us know what you find.
Support for Simulink and (some) toolboxes
One of the most requested features of the previous beta was support for toolboxes and we've made a lot of progress here. Alongside MATLAB itself you'll find the following
- MATLAB
- Simulink
- Signal Processing Toolbox
- Statistics and Machine Learning Toolbox
- Image Processing Toolbox
- DSP System Toolbox
- Parallel Computing Toolbox
- Curve Fitting Toolbox
- Symbolic Math Toolbox
- Communications Toolbox
- Control System Toolbox
- Deep Learning Toolbox
- 5G Toolbox
- LTE Toolbox
- MATLAB Compiler
- MATLAB Compiler SDK
There are some limitations within these. For example Parallel Computing Toolbox's distributed arrays (mentioned in my article on HPC datatypes in MATLAB) don't work, the MATLAB Engine API for Python is not available and so on but a lot of things are supported. Work on all of the other toolboxes not listed above is ongoing of course.
Bench
Let's start by looking at the output of the bench command using a MacStudio with M1 Ultra (20 core),
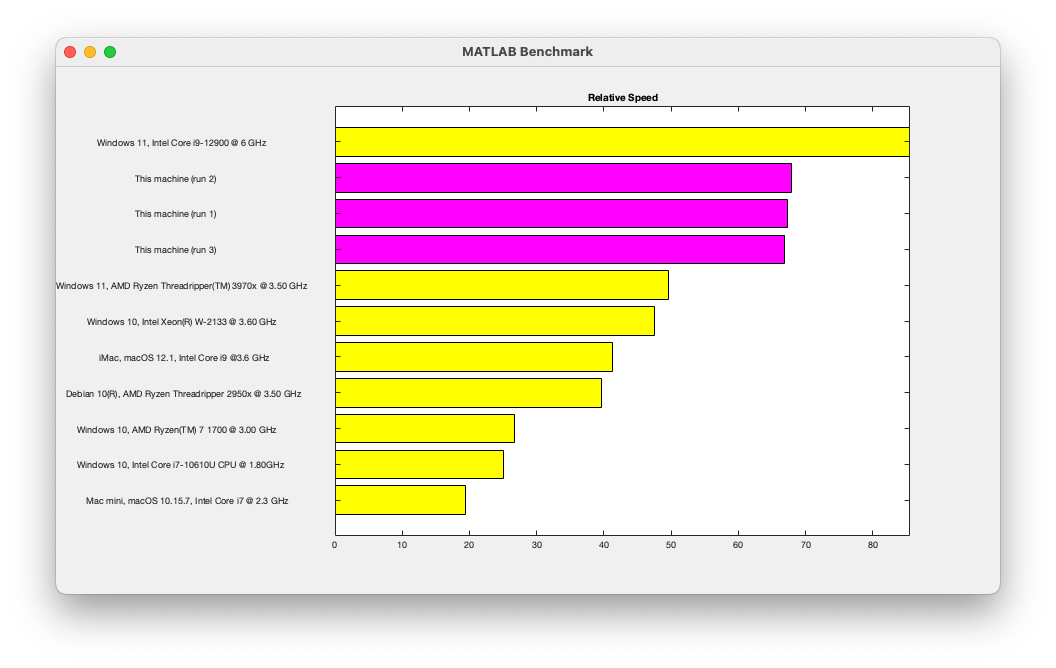
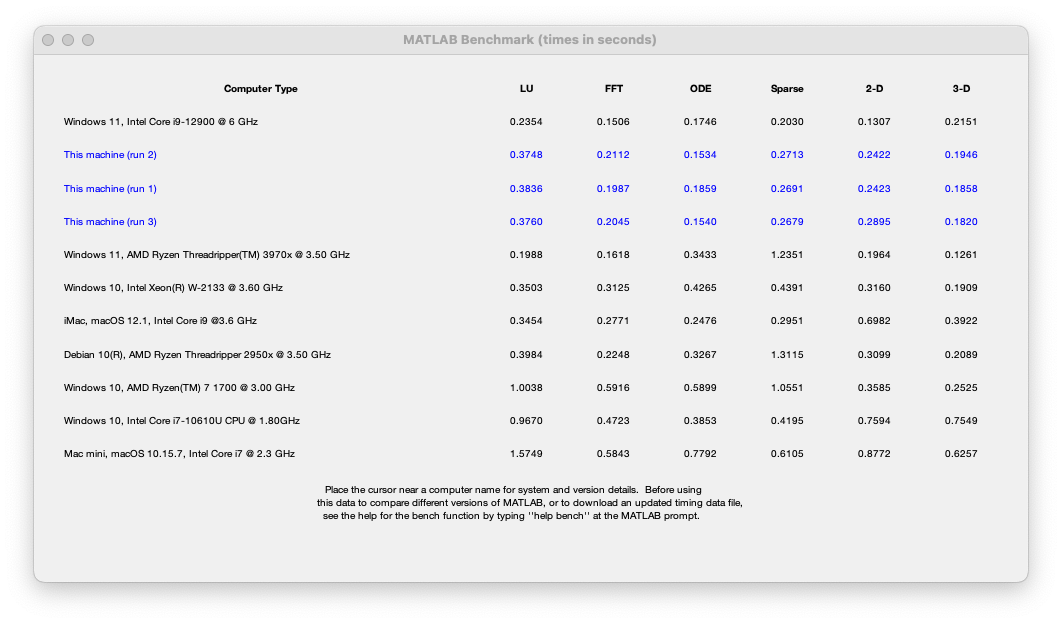
This puts the machine at close to the top of the list of systems reported by Bench. One thing that we've noticed is that the graphics results depend on the resolution of your screen. We are working on this!
More linear algebra results
Bench is great but it only runs one problem size for each computation. This varies with release and for R2022b, the size of the matrix computed by LU is 5200 x 5200 double matrix. You can see this yourself if you look at the source for Bench.
edit bench.m
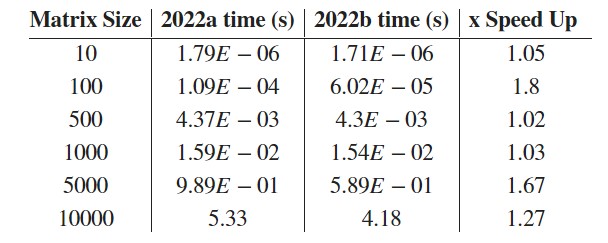
For our internal benchmarking we look at range of matrix sizes in both single and double, real and complex. In double precision, here are the timings on an M1 Ultra (20 cores) in both betas for lu(A) for various sizes of matrix A.

It can be seen that while the new beta is faster for most problem sizes when computing lu(A) (over 4x faster in one case), it is actually a little slower for 500 x 500 matrices. More on this later.
The result closest to the matrices used in R2022b's bench, 5000 x 5000, is 1.3x faster than the previous beta but push the matrix size to 10,000 x 10,000, and all those cores have plenty of work to do. The speed-up in this case is 2.1x compared to the previous beta. Working with large matrices should be a pleasant experience on these machines.
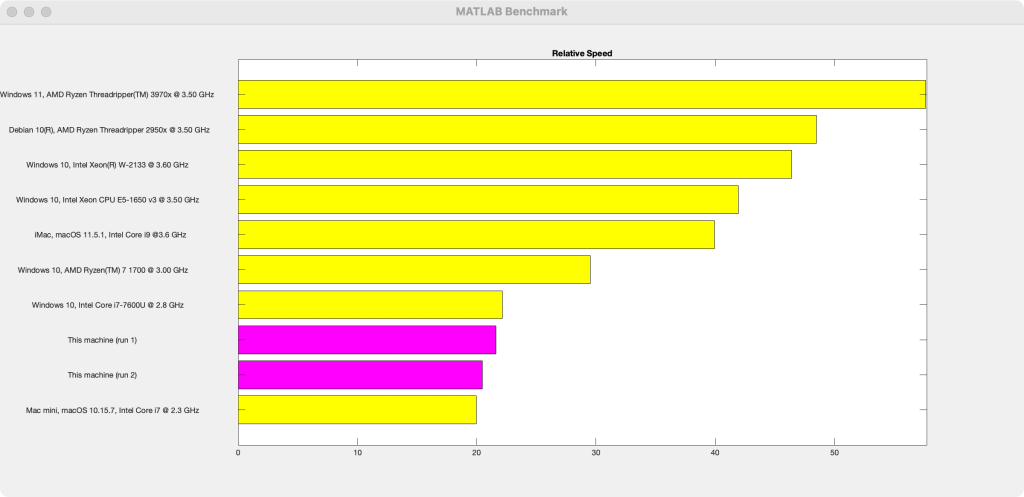
Running the same benchmark on an 8 core M1 Mac Mini gives the following,
In the old beta, the more powerful M1 Ultra was actually slower than an 8 core Mac mini for small matrices (N=10,N=100). This has been fixed for this release but, as mentioned above, there is a problem at N=500 which got slower on the M1 Ultra but stayed at roughly the same speed on the Mac Mini. This is due to us tweaking the thresholds at which multithreading kicks in, a process that is ongoing.
Looking across our internal benchmark results from the two betas I see speed-ups as great as 10x in some cases (e.g. [u,s,v]=svd(R) for single and complex R for R of size 100x50 on an M1 Ultra) but then there is a >5x slow down for inv(symA) (where symA is a double symmetric matrix of size 5000x5000) on the Mac mini and everything in-between. There are many more speed-ups than slowdowns and what you are seeing here is a Work in Progress snapshot of MathWorks' tuning efforts for this hardware.
Why not use Apple Accelerate?
One of the most common questions from my article about the previous beta was "Why not use Apple Accelerate?". LAPACK and BLAS from the Accelerate package were considered (benchmarked even!), but were not chosen for this, or the previous beta, due to its 32-bit integer only support and the fact that it doesn't support the latest version of LAPACK. We continue to monitor the situation and frequently benchmark several BLAS/LAPACK alternatives. We are using what we currently believe (following extensive testing!) to be the best combination for us on this platform.
Over to you
So much for the linear algebra. User musicscientist posted on Reddit that they were 'blown away' by the performance they saw but this is a beta so your mileage may vary. With Simulink and 14 toolboxes also supported, there is a lot to try out so we encourage you to try this beta on your own code and let us know what you find.
- Category:
- Apple,
- performance






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.