Discrete cosine transforms, JPEG, and software compatibility
Software compatibility is a tricky subject. No one likes it when an incompatible change occurs in a software application they rely on. So why do we sometimes find it necessary to make an incompatible change? Here's an illustrative story from the early days of the Image Processing Toolbox.
The function dct2, which computes the two-dimensional discrete cosine transform (DCT), appeared in the original 1993 version of the toolbox. The authors of the toolbox relied on several authoritative references, including Two-Dimensional Signal and Image Processing by Lim. This book contains the following one-dimensional DCT equation:
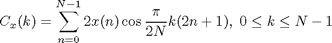
The original implementation of dct2 used this formula.
At roughly the same time as the first toolbox release, the newly-standardized JPEG image compression method and format was becoming popular. The DCT is the mathematical heart of the JPEG algorithm. Here's the 8-point one-dimensional DCT equation that appears in JPEG: Still Image Data Compression Standard by Pennebaker and Mitchell.
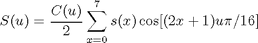
where

The variable name differences are trivial, but the scale factor differences are very important! The JPEG DCT is an orthonormal transform, whereas the DCT defined in Lim's book is not.
Users of version 1 began to contact tech support, wondering why dct2 was giving the "wrong" answer. We realized that we would have to do something, but what? Changing the output of dct2 would introduce an incompatibility. Not changing it would let user confusion and tech support calls continue indefinitely.
We eventually made a decision based on the fact that image compression is the only widespread application of the DCT in image processing. Therefore, it made no sense for our function to produce an answer inconsistent with the standardized DCT-based image compression method. So we changed the output of dct2 in version 2 of the toolbox. When no complaints came in about the change, we breathed a sigh of relief.
Today at The MathWorks we have processes in place to carefully evaluate changes that might result in an incompatibility. What options have the developers considered? What steps are being taken to mitigate possible negative impacts of the change? What is the benefit to the user of the change?
Whether we are doing a good job or not is up to you to judge. How do you think we are doing? How has the evolution of MATLAB over the years affected your work? Have any good stories to tell? Leave your comments here.









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.