Colorful anniversaries in 2006
[Guest blogger Jeff Mather, a developer on the Image and Geospatial team, is also an avid amateur photographer. He published this essay on his personal blog earlier this year and graciously allowed me to reproduce it here. Thanks, Jeff.]
Happy Birthday, CIE Standard Observer
Color is an experience. Colorful light leaves a source of illumination, strikes a surface with its own color properties, and reflects in a different direction. The color of the reflected light is a combination of the illuminant and the colored object, but there's no actual "color" until the light is lucky enough to strike the retina at the back of someone's (or something's) eye.
(Technically, the illuminant has a particular spectral power distribution, or SPD — think of the rainbow and make it brighter in certain parts and darker in others and then compress that thought into one ray of light — and the colorant has its own SPD, which is how likely it is to reflect the different wavelengths of "pure" white light. The reflected light ray has an SPD that is the elementwise product of the two SPDs, which basically means that when white light strikes an object whose SPD is active in the red part of the spectrum, red light is reflected; or when green light strikes a white object, green light is reflected. It also explains why if a more-or-less pure red color strikes an object that doesn't reflect red light, that object appears black — even if it reflects other colors perfectly well. See, linear algebra isn't really that hard!)
While "colorful," reflected light doesn't have any particular color, per se, just the capacity to cause a particular sensation of color. Enter an observer, in particular her eyes and brain. When light strikes the retina, the three types of cone cells there react to the different wavelengths in the SPD in different ways. The combination of the responses from these three cones causes the sensations of redness/greenness, blueness/yellowness, and lightness/darkness which are sent on to the brain. This is the basis of the "opponent theory of color." Remember that term for later.
In turns out that the three cones' responses to color stimuli are fairly easily modelled. Years ago, color scientists had volunteers look at a split screen with a known color — that is, a known SPD — on one side and a tunable set of pure red, green, and blue lights on the other side. The observers changed the color combinations to match the known color. After enough volunteers matched enough colors, it was possible to generalize the visual system's response to all colors into a set of three "cone response functions." In 1931, the CIE standards body published these color matching functions, and the model became known as the "standard observer."
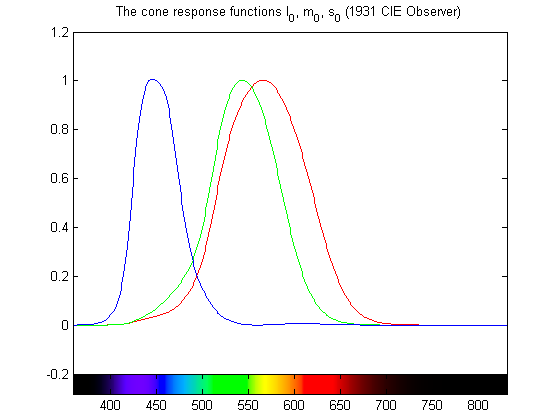
The l, m, and s here correspond to the sensitivies of the long-, medium-, and short-wavelength cones — the red, green, and blue curves, respectively. What's interesting here? Notice how the red and green curves more or less overlap. Timothy King (an anthropology grad student from Stanford) reasons that long-wavelength cones are a recent evolutionary adaptation of medium-wavelength cones, making it possible for us to experience red as a distinct color from green. Also notice that the red curve is steepest where the green curve is flattest, and vice versa; because the cones work together to determine color, this relationship between the cone responses allows for very fine color discrimination.
(In 1964, the CIE published new color matching functions that use a 10-degree visual field, instead of the 2-degree field used in 1931. For perspective, the width of your finger at arms length is approximately one-degree. Turns out, the eye has a different distribution of cones at the fovea than it does a bit further out. Oops! I have included the updated 1964 curves below; but 42-years isn't a good special anniversary, so we'll pretend it didn't happen. Okay?)
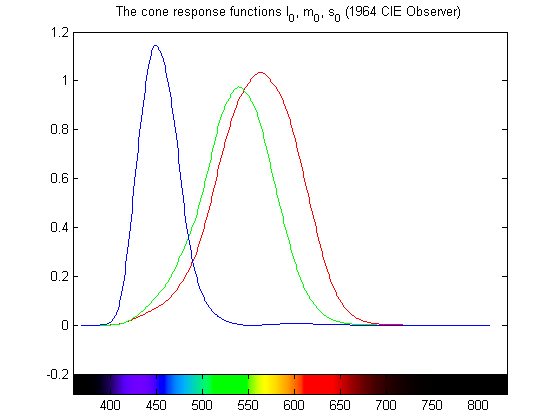
(You can get the MATLAB code to generate cone response functions, label plots with spectral colorbars, convert SPDs to sRGB, and do other color-scientific things on the MATLAB Central File Exchange.)
The standard observer's cone response functions are interesting enough, but hardly worthy of standardization by an industrial illumination group. No, the real power of the standard observer model is the fact that you can take the three cone response curves, combine them with a spectral power distribution (again via linear algebra), and come up with three numbers that tell you exactly what color an object appears to be. It encapsulates many of the complexities of the human visual system and of colorful SPDs and compresses them into three values. The CIE cleverly called this color system "XYZ" — presumably because it's hard to think of any color terms that start with X, Y, or Z.
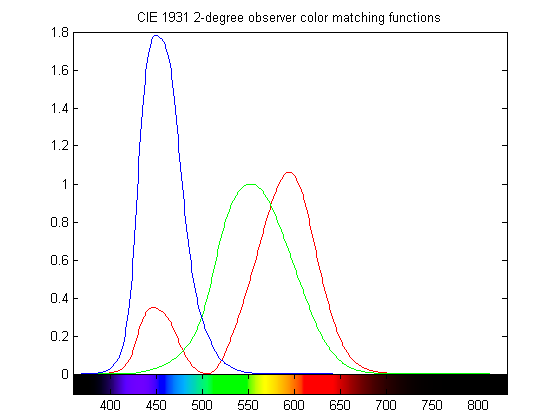
The "color matching functions" that convert an SPD into XYZ appear below. Blue is X, green is Y, and red is Z. It's worth noting that the Y value closely models the overall response to lightness, and that its peak is in the green part of the spectrum. That funny red bump over in the blue end of the spectrum just highlights how XYZ is a constructed model of vision, unlike the cone response functions.
Bon Anniversaire, Monsieur CIELAB
Like any model that squeezes out a lot of information, XYZ isn't perfect; two illuminants with different SPDs can look the same when illuminated by two lamps with different SPDs, for example; that's metamerism. But it does provide a unique way of specifying any observable color, and it's the basis of modern colorimetry and color management systems.
But it's hard to work with XYZ and think about the properties of real colors at the same time. Is that (X,Y,Z) triple more red or green? Dunno. Run it through a separate transformation and find out. What a pain! (Once again, the most fastidious among us usually are the most unpleasant to talk to.) Wouldn't it be great if there were a color system that had the following properties?
- Every color can be expressed
- There's only one way to specify a particular color
- The way to specify that color doesn't depend on the device displaying or observing the color
- It's modelled on the human visual system
- Only three values are needed to express a color
- The three values relate to meaningful values
- It's easy to translate to XYZ and a given RGB triplet
Thirty years ago the CIE — yes the same standards group that created the standard observer model — published CIE L*a*b* (or CIELAB) which aims to satisfy all of those requirements. Every observable color is uniquely represented. The L* value gives the luminance (essentially the brightness) of the color in a perceptually uniform way. The a* and b* values refer to the red-greenness and blue-yellowness of the color, respectively. (Remember the opponent theory of color?) And it's extermely straightforward to map XYZ to CIELAB and back. It's not hard to convert an RGB triplet to CIELAB, either; but unlike L*a*b*, the color of an RGB value depends on the individual values of red, green, and blue that you're talking about — plus a particular color of white. I'll let you wrap your brains around that for a moment.
CIELAB also has the useful property of being more-or-less perceptually uniform. As you move one unit in any direction, the perceived "color difference" is the same (more or less) as a similar move for any other color. How do we know this? Human observers, of course. Sit people down and ask them to quantify the difference between color A and color B. (Personally, I think this would be about as much fun as spending hours changing the perscription in my eyeglasses — "Is one better or Two? A or B?" — but that's the glamorous life of science.)
To Infinity and Beyond!
Anyway, the CIE standard observer and CIELAB present color as a universally describable phenomena. The reality is that it's actually much more complicated. Remember that color depends on a lot of complicated processing in the eye and brain after the cones have been stimulated by light. The color of the thing around an object changes the way we perceive the color of the object itself (regardless of its SPD). Ambient lighting causes our brains to adapt to colors (so-called "white adaptation"). And so on.
Color scientists and the CIE are hard at work to develop "color appearance models," which present a richer (and far more complicated) numerical description of how we perceive color. And maybe next year I will tell you about CIECAM 1997 and 2002.







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.