Fourier transforms
Confession time. When it comes to writing about Fourier transforms on this blog, I'm a chicken. (For my readers not familiar with English slang, chicken in this context means a cowardly or fearful person.)
I'm a chicken because few signal processing topics cause as much confusion, and because few topics seem to inspire as many different, adamant, and sometimes contradictory opinions about the one true way to explain or implement Fourier transform concepts.
The way I see it, the confusion surrounding Fourier transforms stems from four interrelated issues. First, although most people who haven't studied signal processing in depth tend to think there is just one thing called "the Fourier transform," there are actually several. The way I count them, there are four basic types:
- The time domain (or spatial domain for image processing) and the frequency domain are both continuous, infinite domains. There is no explicit or implied periodicity in either domain. This is the one I call the Fourier transform.
- The time domain is continuous and the time-domain functions are periodic. The frequency domain is discrete. I call this the Fourier series.
- The time domain is discrete and infinite, and the frequency domain is continuous. In the frequency domain the transform is periodic. This is the discrete-time Fourier transform (DTFT).
- The time domain and the frequency domain are both discrete and finite. Although finite, the time and frequency domains are both implicitly periodic. This form is the discrete Fourier transform (DFT).
For mathematical analysis of linear time-invariant (or shift-invariant) systems, the Fourier transform and the DTFT are the most useful, depending on whether you are analyzing a continuous-time or discrete-time system. For numerical computation, the DFT is most useful.
The second factor that confuses people is the differing mathematical conventions that are used. The formulas vary in the use of scale factors, the sign in the complex exponential terms, the variables used, and whether sampling period and sampling frequency terms appear explicitly in the equations or are implicit.
The third confusing factor is that the relationships between the different Fourier transform forms can be quite nonintuitive, especially for people not accustomed to thinking in terms of periodic sequences, periodic symmetry, circular shifts, modular indexing, etc.
Finally, there's the confusion caused by the famous FFT acronym. FFT stands for fast Fourier transform, so people expect it to be the Fourier transform, whichever variation they learned. But really it's a fast way to compute one kind of Fourier transform, specifically the discrete Fourier transform.
What finally convinced me to try to write a post involving Fourier transforms was a question received by one of my coauthors of Digital Image Processing Using MATLAB. The questioner wanted to know why the Fourier transform of the image below looked so funny:

I've run out of blog writing time for today, though, so I'll just have to leave you with that teaser. I'll follow up with more about this image and its Fourier transform next time.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building




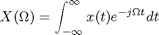


댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.