Discrete-time Fourier transform (DTFT)
In the last two posts in my Fourier transform series I discussed the continuous-time Fourier transform. Today I want to start getting "discrete" by introducing the discrete-time Fourier transform (DTFT).
The DTFT is defined by this pair of transform equations:

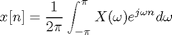
Here x[n] is a discrete sequence defined for all n:
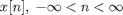
I am following the notational convention (see Oppenheim and Schafer, Discrete-Time Signal Processing) of using brackets to distinguish between a discrete sequence and a continuous-time function. n is unitless. The frequency-domain variable,  , is continuous with units of radians.
, is continuous with units of radians.
Note that  is periodic with period
is periodic with period  .
.
Here are a few common transform pairs:
Unit Impulse
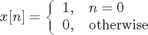

DTFT of Unit Impulse


Rectangular Pulse


DTFT of Rectangular Pulse


Note that the DTFT of a rectangular pulse is similar to but not exactly a sinc function. It resembles the sinc function between
 and
and  , but recall that
, but recall that  is periodic, unlike the sinc function.
is periodic, unlike the sinc function.
Cosine


DTFT of Cosine
The DTFT of a discrete cosine function is a periodic train of impulses:


I updated the above plot on 6-Jan-2010 to show the location of the impulses. -SE
Because of the periodicity of  it is very common when plotting the DTFT to plot it over the range of just one period:
it is very common when plotting the DTFT to plot it over the range of just one period: 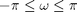 . For example, the DTFT of the rectangular pulse will most often be shown like this:
. For example, the DTFT of the rectangular pulse will most often be shown like this:

Next time I'll discuss the relationship between the continuous-time and the discrete-time Fourier transforms. Until then, Happy New Year everyone!





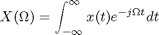


评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。