Plotting the DTFT using the output of fft
In my Fourier transform series I've been trying to address some of the common points of confusion surrounding this topic. For today's espisode I want to look at how to use the fft function to produce discrete-time Fourier transform (DTFT) magnitude plots in the form you might see in a textbook. Recall that the fft computes the discrete Fourier transform (DFT). I described the relationship between the DFT and the DTFT in my March 15 post.
For my example I'll work with a sequence  that equals 1 for
that equals 1 for  and equals 0 elsewhere.
and equals 0 elsewhere.

Here's a plot of the DTFT magnitude of this sequence:
.png)
Now let's see what get using fft.
x = ones(1, 5)
x =
1 1 1 1 1
X = fft(x); plot(abs(X))

Wow, that's not anywhere close to the DTFT magnitude plot above. And why does it look like it's only got two points? Well, take a look at the actual values of X:
X
X =
5 0 0 0 0
We have a 5 and four 0s. What's going on? I explained this back in my March 15 post when I discussed the relationship between the DFT and the DTFT. The outputs of the DFT are samples of the DTFT, and in this case the sample locations just happen to align with the locations of four zeros in the DTFT.
You can get a finer sampling (and a much nicer-looking DTFT plot) by zero-padding. Here I'll use the zero-padding syntax of fft.
N = 256; X = fft(x, N); plot(abs(X))

That's a smoother-looking curve, but it still looks quite a bit different than the DTFT magnitude plot above. To explain the MATLAB output we're looking at, let me show a DTFT magnitude plot that shows three periods instead of just one.
.png)
You can see that the output from MATLAB is one period of the DTFT, but it's not the period normally plotted, which is from
 to
to  . Instead, it's the period from 0 to
. Instead, it's the period from 0 to  . To get a plot from
. To get a plot from  to
to  , use the fftshift function.
, use the fftshift function.
plot(abs(fftshift(X)))

That leaves us with the question of labeling the frequency axis. We want a plot in radians from  to
to  .
.
The way I always remember the frequency scaling between the DFT and the DTFT is this: the length of the DFT corresponds to
the frequency  in the DTFT.
in the DTFT.
So the frequencies in radians corresponding to the output elements of fft are:
w = 2*pi * (0:(N-1)) / N;
But we're calling fftshift to plot the magnitude of the DTFT, so we have to perform a similar shift on our frequencies:
w2 = fftshift(w); plot(w2)

Now our frequencies start at  and have a
and have a  discontinuity in the middle. Here's one way to fix that up:
discontinuity in the middle. Here's one way to fix that up:
w3 = unwrap(w2 - 2*pi); plot(w3)

Now we can redo our magnitude DTFT plot with the x-axis labels.
plot(w3, abs(fftshift(X)))
xlabel('radians')
Often I like to see the multiples of  more clearly along the x-axis. One way to accomplish this is to normalize the frequency variable by
more clearly along the x-axis. One way to accomplish this is to normalize the frequency variable by  .
.
plot(w3/pi, abs(fftshift(X)))
xlabel('radians / \pi')
Another option is to try Alan's pilabels contribution on the MATLAB Central File Exchange.
For the next time, I'm thinking of tackling the question of why the following output is complex:
fft([1 2 3 2 1])
ans = 9.0000 -2.1180 - 1.5388i 0.1180 + 0.3633i 0.1180 - 0.3633i -2.1180 + 1.5388i
Many people expect it to be real.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building


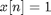




댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.