A Golden Spiral is simulated by a continuously expanding sequence of golden rectangles and inscribed quarter circles.

Contents

Golden Rectangles

We begin with an animated .gif of an imitation Golden Spiral. You can see that removing a square from a golden rectangle leaves a smaller rectangle with the same shape. Connecting inscribed quarter circles produces a continuously expanding spiral. The aspect ratio of the rectangles is the golden ratio.

$$ \phi = \frac{1 + \sqrt{5}}{2} $$

A MATLAB function for generating these expanding golden rectangles and quarter circles is given at the end of this blog post, but this is not a true Golden Spiral.

True Golden Spiral

A logarithmic spiral is a curve given in polar coordinates by

$$ r = \alpha e^{\lambda \theta} $$

The angular coordinate $\theta$ must be multi-valued as the point circles around the origin multiple times. We get the particular logarithmic spiral known as the Golden Spiral by involving the golden ratio and setting

$$ \lambda = \frac{2}{\pi}{\ln{\phi}} $$

Then the radius is scaled powers of $\phi$, with integer powers as $\theta$ crosses the cartesian axes.

$$ r = \alpha \phi^{\frac{2}{\pi} \theta} $$

Here is the plot for $0 \le \theta \le 2 \pi$.

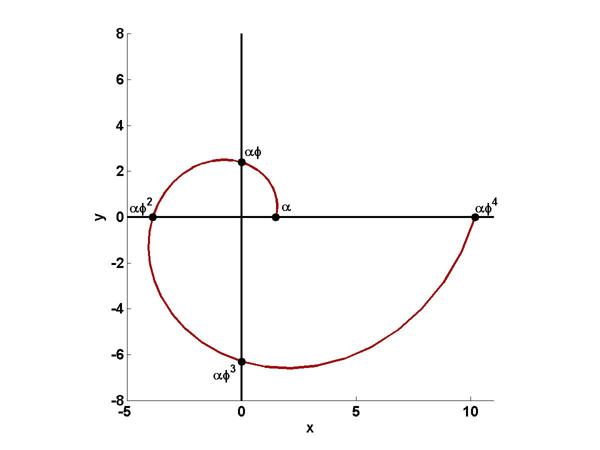
I do not see any obvious analytic way to specify the scale factor $\alpha$. By taking $\alpha$ = 1.48699214 the numeric values generated by the logarithmic Golden Spiral approach those generated by golden rectangles and inscribed quarter circles as the angle $\theta$ gets large.

golden_spiral.m

function golden_spiral
% GOLDEN_SPIRAL  Explosion of golden rectangles.
%    GOLDEN_SPIRAL  Constructs a continuously expanding sequence
%    of golden rectangles and inscribed quarter circles.

%   Copyright 2013 Cleve Moler
%   Copyright 2013 The MathWorks, Inc.

   % Initialize_variables

   % Golden ratio
   phi = (1+sqrt(5))/2;

   % Control speed of zoom
   n = 256;
   f = phi^(1/n);

   % Scaling
   a = 1;
   s = phi;
   t = 1/(phi+1);

   % Centers
   x = 0;
   y = 0;

   % A square
   us = [-1 1 1 -1 -1];
   vs = [-1 -1 1 1 -1];

   % Four quarter circles
   theta = 0:pi/20:pi/2;
   u1 = 2*cos(theta) - 1;
   v1 = 2*sin(theta) - 1;
   u2 = 2*cos(theta+pi/2) + 1;
   v2 = 2*sin(theta+pi/2) - 1;
   u3 = 2*cos(theta+pi) + 1;
   v3 = 2*sin(theta+pi) + 1;
   u4 = 2*cos(theta-pi/2) - 1;
   v4 = 2*sin(theta-pi/2) + 1;

   initialize_graphics

   % Loop

   k = 0;
   while get(klose,'value') == 0
      if mod(k,n) == 0
         power
         switch mod(k/n,4)
            case 0, right
            case 1, up
            case 2, left
            case 3, down
         end
      end
      zoom
      k = k+1;
   end
   pause(1)
   close(gcf)

% ------------------------------------

   function power
      a = s;
      s = phi*s;
      t = phi*t;
   end % power

% ------------------------------------

   function zoom
      axis(f*axis)
      drawnow
   end % zoom

% ------------------------------------

   function right
      x = x + s;
      y = y + t;
      line(x+a*us,y+a*vs,'color','black')
      line(x+a*u4,y+a*v4)
   end % right

% ------------------------------------

   function up
      y = y + s;
      x = x - t;
      line(x+a*us,y+a*vs,'color','black')
      line(x+a*u1,y+a*v1)
   end % up

% ------------------------------------

   function left
      x = x - s;
      y = y - t;
      line(x+a*us,y+a*vs,'color','black')
      line(x+a*u2,y+a*v2)
   end % left

% ------------------------------------

   function down
      y = y - s;
      x = x + t;
      line(x+a*us,y+a*vs,'color','black')
      line(x+a*u3,y+a*v3)
   end % down

% ------------------------------------

   function initialize_graphics
      clf reset
      set(gcf,'color','white','menubar','none','numbertitle','off', ...
          'name','Golden Spiral')
      shg
      axes('position',[0 0 1 1])
      axis(3.5*[-1 1 -1 1])
      axis square
      axis off
      line(us,vs,'color','black')
      line(u3,v3)
      klose = uicontrol('units','normal','position',[.04 .04 .12 .04], ...
         'style','toggle','string','close','vis','on');
      drawnow
   end % initialize graphics

end % golden_spiral

Get the MATLAB code

Published with MATLAB® R2013b

Published with MATLAB® R2013b