Golden Spiral
A Golden Spiral is simulated by a continuously expanding sequence of golden rectangles and inscribed quarter circles.

Contents
Golden Rectangles
We begin with an animated .gif of an imitation Golden Spiral. You can see that removing a square from a golden rectangle leaves a smaller rectangle with the same shape. Connecting inscribed quarter circles produces a continuously expanding spiral. The aspect ratio of the rectangles is the golden ratio.
$$ \phi = \frac{1 + \sqrt{5}}{2} $$
A MATLAB function for generating these expanding golden rectangles and quarter circles is given at the end of this blog post, but this is not a true Golden Spiral.
True Golden Spiral
A logarithmic spiral is a curve given in polar coordinates by
$$ r = \alpha e^{\lambda \theta} $$
The angular coordinate $\theta$ must be multi-valued as the point circles around the origin multiple times. We get the particular logarithmic spiral known as the Golden Spiral by involving the golden ratio and setting
$$ \lambda = \frac{2}{\pi}{\ln{\phi}} $$
Then the radius is scaled powers of $\phi$, with integer powers as $\theta$ crosses the cartesian axes.
$$ r = \alpha \phi^{\frac{2}{\pi} \theta} $$
Here is the plot for $0 \le \theta \le 2 \pi$.
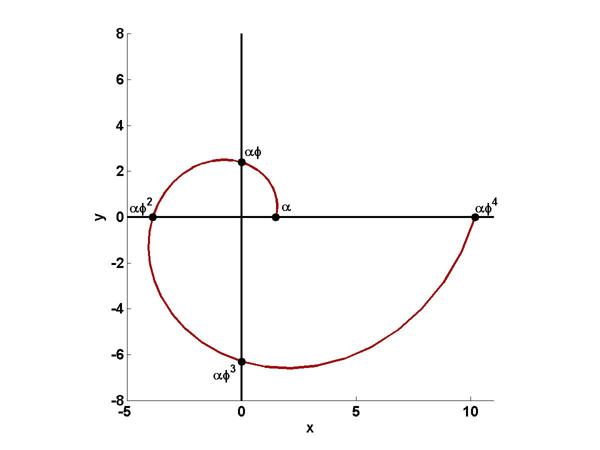
I do not see any obvious analytic way to specify the scale factor $\alpha$. By taking $\alpha$ = 1.48699214 the numeric values generated by the logarithmic Golden Spiral approach those generated by golden rectangles and inscribed quarter circles as the angle $\theta$ gets large.
golden_spiral.m
function golden_spiral % GOLDEN_SPIRAL Explosion of golden rectangles. % GOLDEN_SPIRAL Constructs a continuously expanding sequence % of golden rectangles and inscribed quarter circles.
% Copyright 2013 Cleve Moler % Copyright 2013 The MathWorks, Inc.
% Initialize_variables
% Golden ratio phi = (1+sqrt(5))/2;
% Control speed of zoom n = 256; f = phi^(1/n);
% Scaling a = 1; s = phi; t = 1/(phi+1);
% Centers x = 0; y = 0;
% A square us = [-1 1 1 -1 -1]; vs = [-1 -1 1 1 -1];
% Four quarter circles theta = 0:pi/20:pi/2; u1 = 2*cos(theta) - 1; v1 = 2*sin(theta) - 1; u2 = 2*cos(theta+pi/2) + 1; v2 = 2*sin(theta+pi/2) - 1; u3 = 2*cos(theta+pi) + 1; v3 = 2*sin(theta+pi) + 1; u4 = 2*cos(theta-pi/2) - 1; v4 = 2*sin(theta-pi/2) + 1;
initialize_graphics
% Loop
k = 0;
while get(klose,'value') == 0
if mod(k,n) == 0
power
switch mod(k/n,4)
case 0, right
case 1, up
case 2, left
case 3, down
end
end
zoom
k = k+1;
end
pause(1)
close(gcf)% ------------------------------------
function power
a = s;
s = phi*s;
t = phi*t;
end % power% ------------------------------------
function zoom
axis(f*axis)
drawnow
end % zoom% ------------------------------------
function right
x = x + s;
y = y + t;
line(x+a*us,y+a*vs,'color','black')
line(x+a*u4,y+a*v4)
end % right% ------------------------------------
function up
y = y + s;
x = x - t;
line(x+a*us,y+a*vs,'color','black')
line(x+a*u1,y+a*v1)
end % up% ------------------------------------
function left
x = x - s;
y = y - t;
line(x+a*us,y+a*vs,'color','black')
line(x+a*u2,y+a*v2)
end % left% ------------------------------------
function down
y = y - s;
x = x + t;
line(x+a*us,y+a*vs,'color','black')
line(x+a*u3,y+a*v3)
end % down% ------------------------------------
function initialize_graphics
clf reset
set(gcf,'color','white','menubar','none','numbertitle','off', ...
'name','Golden Spiral')
shg
axes('position',[0 0 1 1])
axis(3.5*[-1 1 -1 1])
axis square
axis off
line(us,vs,'color','black')
line(u3,v3)
klose = uicontrol('units','normal','position',[.04 .04 .12 .04], ...
'style','toggle','string','close','vis','on');
drawnow
end % initialize graphicsend % golden_spiral
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。