ALGOL 60, PL/0 and MATLAB
The 1960 programming language ALGOL 60 influenced the design of many subsequent languages, including C and a miniature language called PL/0. I based the design of the first MATLAB on PL/0.
Contents
ALGOL 58
Algol is a bright, eclipsing three-star system in the constellation Perseus. It provides the name of a family of "algorithmic" programming languages developed very early in the computer era by an international group of, primarily, mathematicians.
I do not have room here to describe ALGOL. Let me just say that ALGOL has profoundly affected my professional life.
In the first published report in 1958, the programming language was originally called IAL, for International Algebraic Language. There were eight authors of the report, including John Backus, an American who headed the IBM team that developed the original Fortran; Friedrich Bauer, a German who was the subject of my previous blog post; and Heinz Rutishauser, a Swiss numerical analyst who invented the LR algorithm.
We had two of versions of ALGOL 58 at Stanford when I was a grad student there in the early '60s. Burroughs had their BALGOL on the B220. We used that for the beginning programming course for about a year. Then two students, Larry Breed and Roger Moore, implemented BALGOL on the new campus IBM mainframe, the 7094. We called it SUBALGOL and used it heavily, including in the programming courses, for a couple of years.
JOVIAL
One of my all-time favorite acronyms is JOVIAL, for Jules Own Version of International Algebraic Language. It was developed beginning in 1959 by a group headed by Jules Schwartz at SDC, System Development Corporation. JOVIAL and it successors were in use for almost fifty years by US military projects.
ALGOL 60
ALGOL, short for Algorithmic Language, was presented in a 1960 report with thirteen authors and edited by Danish computer scientist Peter Naur. The report summarized almost everything that was known about the design of programming languages at the time, which was barely ten years after the development of the first stored program computers. Wikipedia has this to say about ALGOL's influence.
It was the standard method for algorithm description used by the ACM in textbooks and academic sources for more than thirty years. In the sense that most modern languages are "algol-like", it was arguably the most successful of the four high-level programming languages with which it was roughly contemporary: Fortran, Lisp, and COBOL.
ACM Algorithms
The ACM began publishing collections of scientific algorithms in 1960. The collected algorithms appeared in Communications of the ACM (CACM) until 1975 when Transactions on Mathematic Software (TOMS) began publication and took over the collection. Initially, all the contributions were required to be in ALGOL 60. Fortran was permitted after it was standardized in 1968. The last ALGOL submission was in 1977. In more recent years, even some MATLAB programs have been accepted.
In the early years of the ACM algorithms section, Stanford played an important role in the editorial process. George Forsythe, who was the founding chairman of Stanford's Computer Science Department and my Ph. D. advisor, was also President of ACM at one time and editor of the algorithms section at another.
My grad school buddy, Bill McKeeman, contributed a couple of early algorithms, in ALGOL. One is algorithm 135, a linear equation solver, "Crout with equilibration and iteration". The Crout algorithm computes the LU factorization from the inner product description of the matrix elements. Another is algorithm 145, "Adaptive numerical integration by Simpson's rule". This one uses recursion even though our BALGOL compiler at Stanford at the time could not handle recursion and Bill could not actually run his program. When we did acquire a Burroughs B5000 with a full ALGOL compiler, Bill verified that his recursive program would work within hours of the machine's installation. (Many years later, one of McKeeman's crowning achievements is the current version of the MATLAB why function, which also uses recursion.)
My first ever professional publication is "Remark on Certification of Matrix Inversion Procedures" in the Algorithms section of the July 1963 CACM. It is in response to a contribution by Peter Naur, the editor of the ALGOL 60 report. Naur, who was not a numerical analyst, had made the common mistake of comparing the computed inverse of the floating point approximation to the Hilbert matrix to the known inverse of the exact Hilbert matrix. The difficulty is that the effect of the initial floating point approximation is larger than the effect of the rounding errors in the inversion.
Example
For an example of an ALGOL procedure, let's take a look at SOLVE, a program from Computer Solution of Linear Algebraic Systems, the 1967 textbook by Forsythe and myself. We have programs in this book in ALGOL, Fortran, and PL/1. This program is preceded by DECOMPOSE, a longer program that computes the LU decomposition. Reading these programs today, I'm surprised to see that I used a global array to store the pivot indices. These programs are in the publication format which uses bold face characters for the key words.

Numerische Mathematik
In the late 1960s the journal Numerische Mathematik ran a series of research papers about numerical linear algebra that includes ALGOL procedures. Altogether there are 29 papers by a combined total of 19 authors. Sixteen of the papers are by J. H. Wilkinson and coauthors. In 1970 all of the papers, with a few modifications, were collected in a volume edited by Wilkinson and C. Reinsch titled "Handbook for Automatic Computation, Volume 2: Linear Algebra". (I'm not sure if Volume 1 of this intended larger project was ever written or published.)
EISPACK
ALGOL was always intended to be a language for research and publication, not for actual execution. IBM dominated the computer market in the '60s and '70s, certainly in the US, and IBM did not support ALGOL. Moreover, in its standard form, ALGOL 60 had no provision for input and output. So it was always expected that the algorithms published by the ACM and Numerische Mathematik would have to be modified or translated to some other language before they could actually be used.
The NATS Project, the National Activity to Test Software, was a project at Argonne National Laboratory whose focus was the testing, certification, distribution, and support of mathematical software. Most of the investigators were Argonne staff. I visited Argonne in the summer. The Algol procedures in the Numerische Mathematik linear algebra series were organized in two parts. The second part dealt with matrix eigenvalue problems. We translated the procedures in part two to Fortran, carefully preserving their structure and numerical properties. We then tested and timed them at about twenty university and national laboratory sites, and made the collection publically available. "Certification" consisted of a carefully worded offer to respond to any reports of poor or incorrect performance.
The result was EISPACK, for Matrix Eigensystem Routines. We published the Users' Guide in three parts in the 1970s. Numerische Mathematik and the Wilkinson/Reinsch Handbook had been published by the German publisher Springer-Verlag and we regarded EISPACK as a translation project, so published our guides with them as well.
LINPACK
EISPACK was followed at Argonne by another project, LINPACK, to produce a package for solving linear equations and related problems. Together, the two packages would provide a fairly complete set of routines for computations involving dense matrices. LINPACK was not a NATS project and did not have immediate ALGOL antecedents.
Niklaus Wirth
Niklaus Wirth is a Swiss computer scientist who received his PhD from Berkeley in 1963, was on the Stanford faculty at the time the Computer Science department was created in 1965, and returned to the ETH in Switzerland in 1968.
While he was at Stanford, Wirth and Tony Hoare proposed some modifications and simplifications of ALGOL 60 that made it easier to compile and practical for actual execution. The IFIP working group on algorithmic languages felt that the proposal was not a sufficient advance over ALGOL 60, but Wirth implemented it nevertheless. The result became known as ALGOL W, "W" for Wirth, and was used in many programming courses for a number of years.
Wirth is probably best known for his language PASCAL, another descendant of ALGOL. Introduced in 1970, PASCAL is one of the first languages to provide structured programming and data structures. PASCAL proved to be very popular on personal computers in the 1980s.
PL/0

In 1976 Wirth published a textbook, Algorithms + Data Structures = Programs. The last chapter is "Language Structures and Compilers". Wirth gives a formal definition of a miniature programming language that he calls PL/0. He describes how to parse PL/0 and generate code for a hypothetical machine.
PL/0 has only one data type, integer. Wirth defines PL/0 with the seven syntax diagrams for program, block, statement, condition, expression, term, and factor. Here are three of those diagrams.
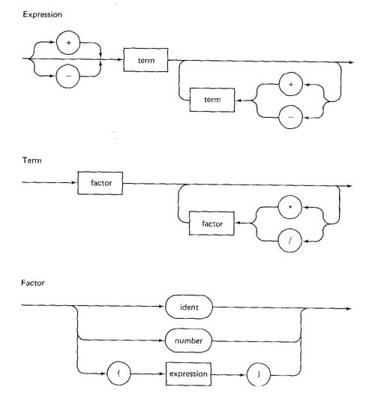
These definitions are recursive. An expression consists of terms separated by additive operators. A term consists of factors separated by multiplicative operators. And a factor consists of identifiers, numbers, or expressions in parentheses.
The syntax diagram for statement introduces begin, end, if, then, while, do, and call. The diagram for block introduces procedure. And the diagram for condition involves relational operators. So, despite the simplicity of the definitions, there is a rich structure.
At the time, I was at professor at the University of New Mexico, teaching courses in linear algebra and numerical analysis. I wanted my students to have access to LINPACK and EISPACK without writing Fortran programs. Almost as a hobby, I used Wirth's chapter to develop a simple Matrix Laboratory. Consequently, the syntax of the original MATLAB is that of PL/0. I will discuss this in more detail in my next blog post.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。