I recently published Round, With Ties to Even and followed that with Round Two. Then, in an email, Andy Bartlett pointed out that my new round function fails for some large values of x between flintmax/2 and flintmax.

Contents

flintmax/2

The quantity f = flintmax/2 is equal to 2^52, which is 1/eps. The help entry for format bank says it is a fixed format for dollars and cents. That's true, but I also like to use it for displaying large flints.

   format bank
   f = flintmax/2

f =
 4503599627370496.00

The numbers in the interval [f flintmax] are the largest flints. They are all integers. The spacing between them is one.

   eps(f)

ans =
          1.00

All floating point numbers larger than flintmax are integers, but the spacing between is larger than one, so they cannot be used for integer arithmetic.

Rounding

The idea behind all versions of round is the following. Suppose abs(x) is between two integers, y-1 and y. Then

   a = abs(x) + 0.5;

is between y-0.5 and y+0.5. And

   r = floor(a);

is equal to either y-1 or y, whichever is closer to abs(x).

That idea works for almost all x. However, if x is between f and flintmax, the quantity x + 0.5 is not a floating point number and must itself be rounded to the nearest even by the addition hardware. If y is odd, the resulting a will be y+1, which is too large.

So, I must compute a by

   a = abs(x) + (0.5 - eps/4);

The quantity (0.5 - eps/4) is the next smaller floating point number less that 0.5.

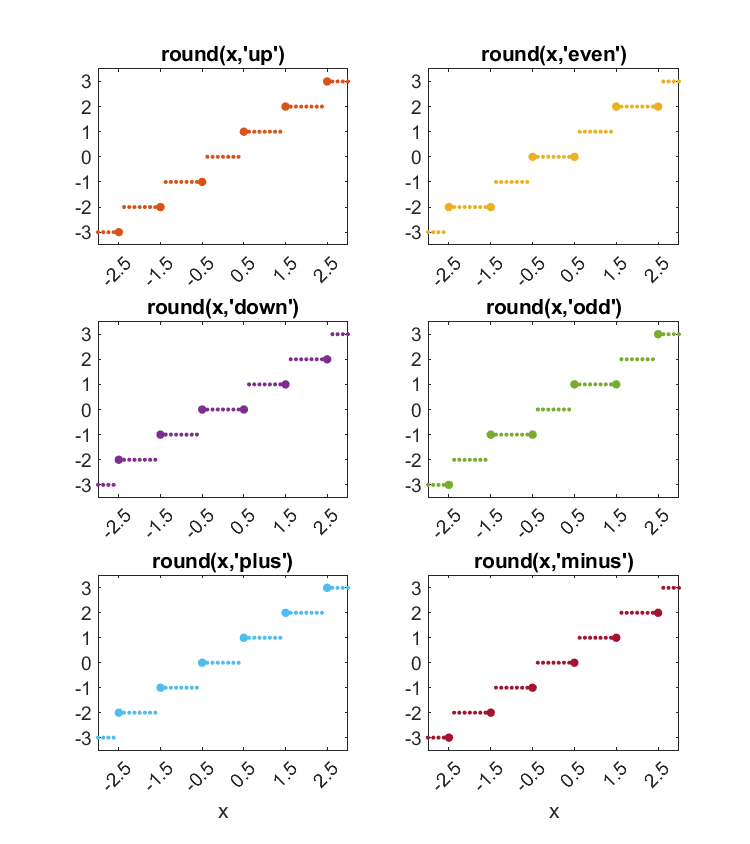
round

This is the resulting proposal for the enhancement request on round. It is available here. Only the line computing a has changed from Round Two.

   type Round.m

function r = round(varargin)
% r = round(x) scales and rounds the elements of x to the nearest integers.
% Default: ties, elements halfway between integers, are rounded away from zero.
%
% r = round(x,'even') ties round to even integers.
% r = round(x,'odd') ties round to odd integers.
% r = round(x,'up') ties round away from zero (same as default).
% r = round(x,'down') ties round towards zero.
% r = round(x,'plus') ties round to the right on the number line.
% r = round(x,'minus') ties round to the left on the number line.
%
% r = round(x,n), n >= 0, round(10^n*x)/10^n, round(12.3456,2) = 12.3500        
% r = round(x,-n), n > 0, 10^n*round(x/10^n), round(1234.56,-2) = 1200.
% r = round(x,n,'significant'), round(.001234,2,'significant') = .0012
% r = round(x,n,'decimals) same as round(x,n).
%
% r = round(x,...), ties, n, 'significant' and 'decimals' can be in any order.
%
% Use Round(...) with capital R to distinguish from built-in round(...).

    [x,n,ties] = parse_input(varargin{:});
    x = prescale(x,n);
    
    a = abs(x) + (0.5-eps/4);
    r = floor(a);
        
    switch ties
       case 'even'
           m = (r == a) & (mod(r,2) == 1); 
       case 'odd'
           m = (r == a) & (mod(r,2) == 0);
       case 'down'
           m = (r == a);
       case 'up'
           m = [];
       case 'plus'
           m = (x < 0) & (r == a);
       case 'minus'
           m = (x > 0) & (r == a);
       otherwise
           error(['''' ties ''' not recognized.'])
    end
    r(m) = r(m) - 1;
    r = sign(x).*r;

    r = postscale(r,n);
   
    % ----------------------------------------------
   
    function [x,n,ties] = parse_input(varargin)
        x = varargin{1};
        n = zeros(size(x));
        ties = 'up';
        for k = 2:nargin
            if isnumeric(varargin{k})
                n(:) = varargin{k};
            elseif strcmp(varargin{k},'significant')
                n(:) = n(:) - ceil(log10(abs(x(:))));
            elseif strcmp(varargin{k},'decimals')
                % ignore
            else
                ties = varargin{k};
            end
        end
    end
   
    function x = prescale(x,n)
        if any(n ~= 0)
            k = n > 0;
            x(k) = 10.^n(k).*x(k);
            k = n < 0;
            x(k) = x(k)./10.^(-n(k));
        end
    end
 
    function r = postscale(r,n)
        if any(n ~= 0)
            k = n > 0;
            r(k) = r(k)./10.^n(k);
            k = n < 0;
            r(k) = 10.^(-n(k)).*r(k);
        end
    end
end

test

The vector x = f:flintmax would have 2^52+1 elements. That's too many. The first four and the last four is enough.

    format hex
    x = [f+(0:3); 2*f-(3:-1:0)]
    r = Round(x)
    up = Round(x,'up')
    down = Round(x,'down')
    even = Round(x,'even')
    odd = Round(x,'odd')
    plus = Round(x,'plus')
    minus = Round(x,'minus')

x =
   4330000000000000   4330000000000001   4330000000000002   4330000000000003
   433ffffffffffffd   433ffffffffffffe   433fffffffffffff   4340000000000000
r =
   4330000000000000   4330000000000001   4330000000000002   4330000000000003
   433ffffffffffffd   433ffffffffffffe   433fffffffffffff   4340000000000000
up =
   4330000000000000   4330000000000001   4330000000000002   4330000000000003
   433ffffffffffffd   433ffffffffffffe   433fffffffffffff   4340000000000000
down =
   432ffffffffffffe   4330000000000000   4330000000000001   4330000000000002
   433ffffffffffffc   433ffffffffffffd   433ffffffffffffe   433fffffffffffff
even =
   4330000000000000   4330000000000000   4330000000000002   4330000000000002
   433ffffffffffffc   433ffffffffffffe   433ffffffffffffe   4340000000000000
odd =
   432ffffffffffffe   4330000000000001   4330000000000001   4330000000000003
   433ffffffffffffd   433ffffffffffffd   433fffffffffffff   433fffffffffffff
plus =
   4330000000000000   4330000000000001   4330000000000002   4330000000000003
   433ffffffffffffd   433ffffffffffffe   433fffffffffffff   4340000000000000
minus =
   432ffffffffffffe   4330000000000000   4330000000000001   4330000000000002
   433ffffffffffffc   433ffffffffffffd   433ffffffffffffe   433fffffffffffff

Get the MATLAB code

Published with MATLAB® R2021a