Lights, Camera, Action — and Sound
I am very excited to incorporate sound in animations. This blog post has five examples with links to videos enclosed in '+ + + +'.
Contents
Mertens
I began making animations with sound while investigating the Mertens Conjecture. The OEIS page offers an opportunity to listen to the Mertens sequence, but I wanted more control.
The resample function is the Signal Processing Toolbox resamples a signal at a fraction, p/q, times the original sample rate. The sound in this Mertens example is generated from a recording of piano playing middle C that is resampled to simulate the other notes.
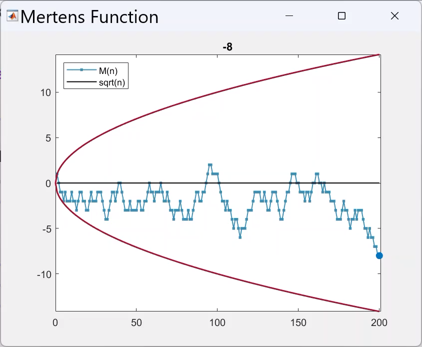
Here is a link to a 40-second video of M(n) and sqrt(n) for n = 200. (Homework: How long would the video last if n = 10^8? Post your answers in the comments.)
+ + + + + + + + + + + + + + + + + + + + + + + + + + +
https://blogs.mathworks.com/cleve/files/mertens.mp4
+ + + + + + + + + + + + + + + + + + + + + + + + + + +
Here is a static graphic, the last frame of the video.
Lissajous
You may well have seen Lissajous curves before, but have you ever listened to them? They were first studied extensively by Jules Lissajous, a nineteenth-century French physicist. There are many Lissajous curves similar to the following, where the trajectory in the x-y plane is described by two functions of a parameter t.
n = 200; t = 3*pi*(-1:2/n:1); x = 5*cos(t)+3*cos(5/3*t); y = 5*sin(t)-sin(5/3*t);
This 40-second video employs sound produced by resampling a note from a xylophone.
+ + + + + + + + + + + + + + + + + + + + + + + + + + +
https://blogs.mathworks.com/cleve/files/lissajous.mp4
+ + + + + + + + + + + + + + + + + + + + + + + + + + +
Here is the last frame.

tansin
I have used variations of this function many times.
F = @(x) tan(sin(x))+sin(tan(x));
When x approaches an integer multiple of pi, both sin(x) and tan(x) approach zero, so F(x) also approaches zero. But when x approaches an odd multiple of pi/2, tan(x) becomes infinite, so both sin(tan(x)) and F(x) oscillate infinitely often.
Here is a link to a 45-second video of F(x) for n = 200 evenly spaced values of x between -2pi and 2pi. If we increase n, we would see more of the oscillations at the singularities. The sound comes from resampling a single note played by a trumpet.
+ + + + + + + + + + + + + + + + + + + + + + + + + + +
https://blogs.mathworks.com/cleve/files/tansin.mp4
+ + + + + + + + + + + + + + + + + + + + + + + + + + +

Van der Pol
Quoting Wikipedia.
In the study of dynamical systems, the van der Pol oscillator (named for Dutch physicist Balthasar van der Pol) is a non-conservative, oscillating system with non-linear damping.
In this video, we see -- and hear -- the numerical solution, computed by ode45, of the Van der Pol equation at n points between t = 0 and t = 20. The damping parameter is mu = 2.
The sound comes from a recording of a student practicing a piano. In this case we have scales spanning four octaves, so no resampling is required.
+ + + + + + + + + + + + + + + + + + + + + + + + + + +
https://blogs.mathworks.com/cleve/files/vanderpol.mp4
+ + + + + + + + + + + + + + + + + + + + + + + + + + +

Blackjack
The card game Blackjack is another example that I use frequently; see "Simulating Blackjack" and MATLAB file exchange. The video shows a simulation of a few hundred hands, starting each hand with a $10 bet. The sound comes from a piano playing a C-major scale. Again, resampling is not necessary.
The emerging histograms in the video, and the static outcome in the final frame, show the percentages observed for each of ten possible outcomes. The histograms can be compared with those in the "Simulating Blackjack" article that describes the use of the Parallel Computing Toolbox to play 10,000 hands with these results.
bjpercent
" Push, player and dealer have equal totals not exceeding 21 "
" Win, player's total is greater than dealer's and does not exceed 21 "
" Lose, dealer's total is greater than player's and does not exceed 21 "
" Blackjack, player has 21 with two cards, dealer does not "
" "
" $-40 0.03 Split and double, lose both "
" $-30 0.17 Split and double, lose one "
" $-20 4.71 Split or double, lose "
" $-10 42.94 Lose "
" $ 0 9.06 Push "
" $+10 32.13 Win "
" $+15 4.44 Blackjack "
" $+20 6.19 Split or double, win "
" $+30 0.28 Split and double, win one "
" $+40 0.06 Split and double, win both "
(Homework. This simulation happens to have three hands with the very rare swings of more than $20. Find the hand numbers where such rare events occur. Post your answers in the comments. Hint: watch the emerging histograms.)
+ + + + + + + + + + + + + + + + + + + + + + + + + + + +
https://blogs.mathworks.com/cleve/files/blackjack.mp4
+ + + + + + + + + + + + + + + + + + + + + + + + + + + +











コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。