Last month we collaborated with Luke Rendell and Elena Miu of St Andrews University on a programming contest (hosted at CumulusContest.org). This contest was modeled on our old MATLAB programming contest.

My job was to come up with a challenge. Here it is: take a chain and coil it on the floor of a box. For instance, suppose I gave you this chain. Each link, or bead, is drawn a different size to indicate that it has a different weight.

Your job is to place the chain in the box compactly; that is, with the heavy bits bunched in the middle as much as possible. Even so, the chain must lie in a single plane and snake through the box using only straight segments or 90 degree turns.

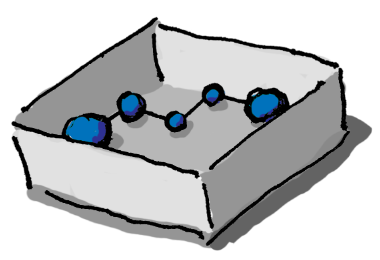
Here’s an example built with MATLAB code. How would you arrange this chain?

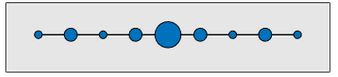
You can see easily enough that we want to put the heaviest weight right in the middle. So the optimal weight distribution looks like this.

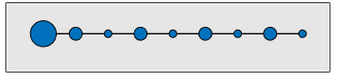
But now suppose you were given this chain. It’s the same weights, but in a different order.

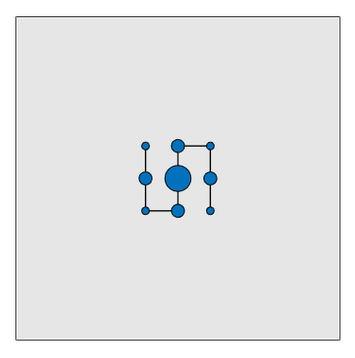
The optimal weight distribution is the same, but the snaking path of the chain is different.

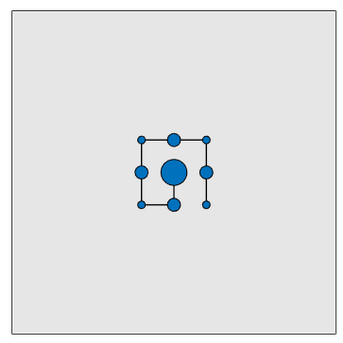
So you get the basic idea. But the problem gets much harder to solve as the chain gets longer. Given this chain, how would you write an algorithm to fold it quickly and efficiently?

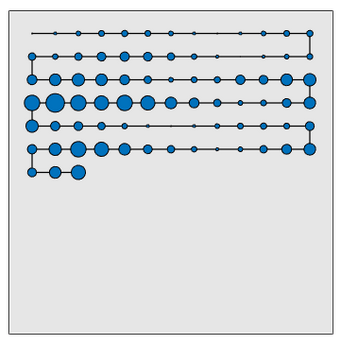
Here’s what the winner of the contest generated. Not bad!

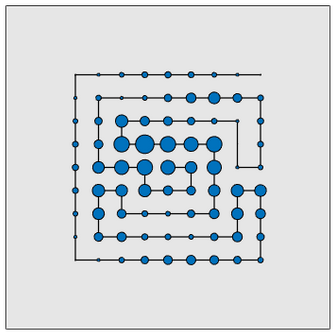
It’s a fiendish problem. Participants of the contest couldn’t afford to test their answers exhaustively. For one thing, combinatorics being what they are, there isn’t enough time in the universe to be completely exhaustive. For another thing, we gave them only 50 seconds to solve more than 100 of these problems.

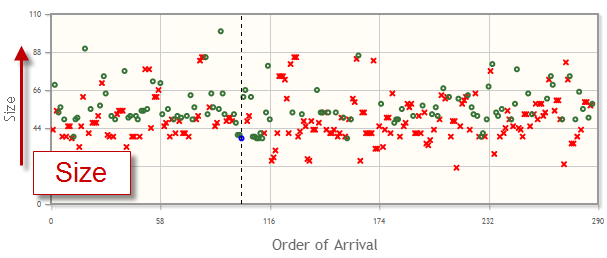
I’m so impressed with the people who coded up solutions. Not just solutions, but lots of them, and lots of good ones. And they’re all available for your inspection on the site. Here is a plot of all the entries. There were 1148 total entries, of which 841 passed and received scores. Among these passing entries were 89 leaders.

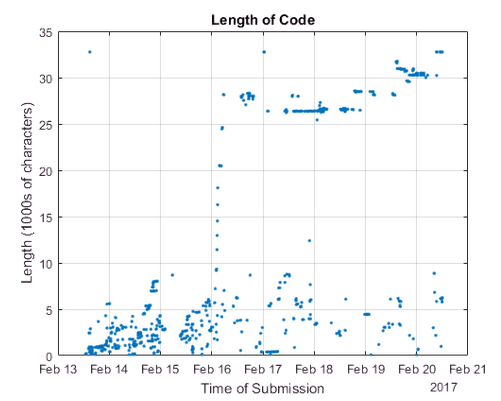
That red line running along the bottom goes through each of the leaders. The algorithms started out small, but they grew as the contest progressed. Here’s a plot of code size over time.

I’ll finish with an animation of an especially entertaining kind of chain: a collection of equal weights separated by long empty stretches of cable. It made for some beautiful maze-like results. Here’s the starting chain. How would you cluster those beads in the middle?

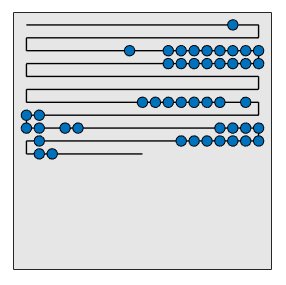
Below is an animation of the results achieved by 24 different leading algorithms. I’m not showing all the leaders because many of them were speed improvements that didn’t change the layout of the chain.

Stay tuned… I understand the folks at St Andrews want to run more contests! When they do, I’m sure they’ll announce it over on their CumulusContest site.

And as always, thanks to everyone who played!