I like to play Cody because I always learn something. After I've solved a problem, I spend a little time with the Solution Map looking at other solutions. It doesn't take long to find something better, and often I learn about a function that I never knew existed.

For instance, have you ever heard of the function ISSORTED? It's a simple function, but it was new to me. Let me tell you how I first learned about it. Along the way, I'll tell you about a new trick for finding good Cody solutions.

Let's consider Cody Problem 10, which is about monotonically increasing vectors. Here's the problem statement: Return true if each element in the input vector is larger than its predecessor.

At the moment I write this, Problem 10 has over 67,319 solutions. Quick! Which one is the best? It's a daunting request. But the best solution out of a set that big is probably pretty good. Certainly worth a look. But which one is it?

We can start with a simple distinction: of all these solutions, only 20,813 are correct. So that's progress! The best solution is likely to be in this subset. Which of these correct answers is the best? Cody uses a metric, called "size," to rank the solutions. A solution's size is the number of nodes in the parse tree for a given solution, and lower is considered better. It's a useful metric, but far from perfect. We all know that the shortest solutions aren't always the best solutions. Indeed, because of some weird hacks that people have worked out (cough cough, regexp), the shortest solution is often a terrible solution in real life.

If size isn't a great metric, can we come up with a better one? In general, it's difficult, maybe impossible, to come up with an automated system that can figure out which solution is the best. What criteria are you using? Size? Speed? Efficiency? Readability? And how do you weight each of these? Would you sacrifice readability for the sake of speed, or vice versa? Everybody has a different notion of goodness.

Ultimately, what most of us want to know is this: Which solution do most people prefer? It's a utilitarian answer that relies on the wisdom of the crowd. We're acknowledging that judging code is subjective, and we're asking our friends and neighbors to apply their subjectivity, biases and all. This turns out to work pretty well.

Head-to-Head Ranking

Now that we've decided to make a subjective judgment system, we have to work through some practical issues. How do you get people to give fair and distinct scores to thousands of solutions? Here is the key insight: whereas it's difficult to grade individual entries consistently, it is generally straightforward to compare two entries and say which one is better. And once we've built up enough binary comparisons, we can use statistics to work out scores for all the solutions. Here we rely on techniques (the Bradley-Terry algorithm, in this case) developed for ranking players in sports and games. Think about how a collection of chess or tennis matches can be aggregated into one global ranking.

A few months ago, Cody added a crowd-scoring feature based on this head-to-head comparison approach. Now we can tell you not only which code is the smallest, but also which code is preferred by the people who are playing.

Let's look at a set of solutions to Problem 10 that have all been ranked. Here is a histogram by size. The median size is 37.

Things get more interesting when we plot crowd score vs. size. Crowd score is what we're calling the subjective ranking applied by players like you. This number is the output of the Bradley-Terry algorithm, and it's been normalized here so that the best crowd score is 100.

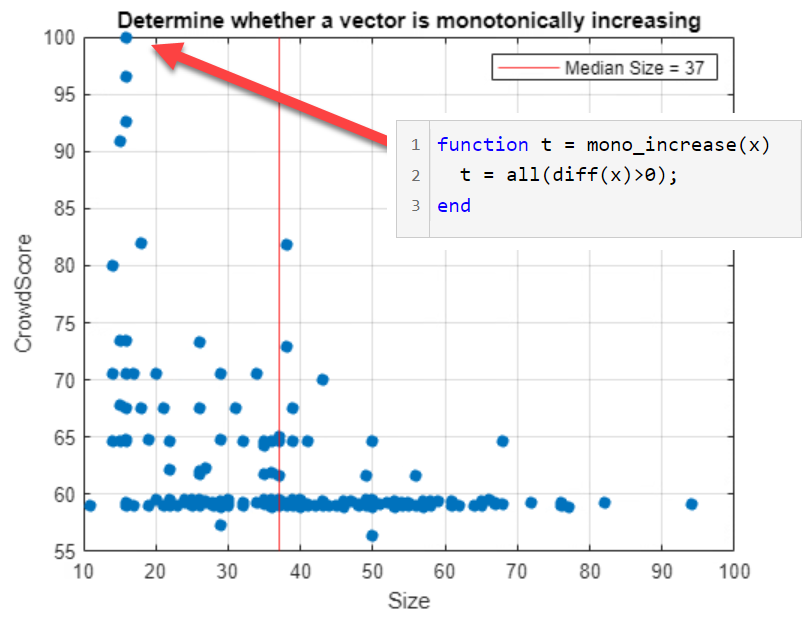
There is an obvious skew to the distribution: preferred solutions tend to be shorter.

We should note here that the great majority of solutions have not been given a crowd score yet, so we can't expect the results to be comprehensive and consistent. Similar entries may receive different ratings. Nevertheless, the plot is instructive. It extracts good entries from the vast amount of background noise.

The red arrow indicates the current crowd favorite:

In English we might say: in all cases, the difference between two successive elements should be positive. Compact and easy to read! This use of DIFF is a nice example of vectorized code. You don't need a loop to go through all the elements of x. But you can if you want to. Here is a longer, less preferred solution.

It still gets the correct answer, but the code is longer (and arguably, harder to read) because it explicitly loops through the vector x.

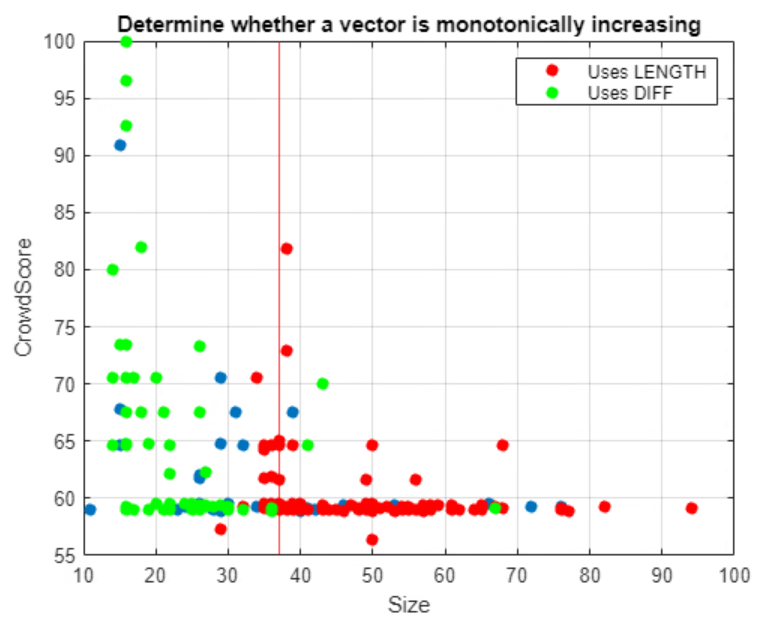
Here is a plot that distinguishes between those solutions that use the vectorized DIFF approach and those that use the looping LENGTH approach. Vectorization leads to shorter, and generally more preferred code.

There are many variants on the DIFF theme. For instance, this one is slightly more complicated than the leader.

Here's one that is still vectorized, but it does the DIFF calculation explicitly.

There are some other intriguing entries from the list of preferred solutions. I like this one. Here the function UNIQUE is enforcing the problem criteria: if the vector is already in the order that would be returned by UNIQUE, then you're good.

And finally, here's the one from farther down the list that took me by surprise.

I didn't even know about the ISSORTED function, but it's been around for a long time, and it offers the shortest, most direct solution to the problem.

Which one of these is your favorite, and why?

I love solution tourism in Cody. Where else can you be exposed to so many novel functions and solution methods? Even so, the full list of Cody solutions can feel like an impenetrable jungle. Where do you start? That's why we introduced solution voting: to find the treasures hidden in the thicket.

And if you like this feature, remember that it's only as good as the votes going into it. Please spend a little time voting on answers yourself. It only takes a little effort, and everybody wins!