Evolution of logical arrays in MATLAB
An internal design discussion this week prompted me to reflect on the history of logical arrays in MATLAB. Because the Image Processing Toolbox treats logical arrays as binary images, their behavior and use is important to those of us who develop (and use!) the product.
If you travel back in time to 1996, MATLAB had only a single type: the two-dimensional, double-precision matrix. No multidimensional arrays, integer arrays, char arrays, cell arrays, struct arrays, or logical arrays. You could define any type you wanted as long it was 2-D double.
But if you go back ten years earlier to 1987, you'll find that an important MATLAB "logical" behavior existed even then: logical indexing. Basically, logical indexing was defined back then as expression of the form A(B), where B was the same size as A and contained only 0s and 1s.
Below is a screen shot from MATLAB 3.13, which was the earliest version of MATLAB I ever used. (Amazingly, it still runs on my computer today!)
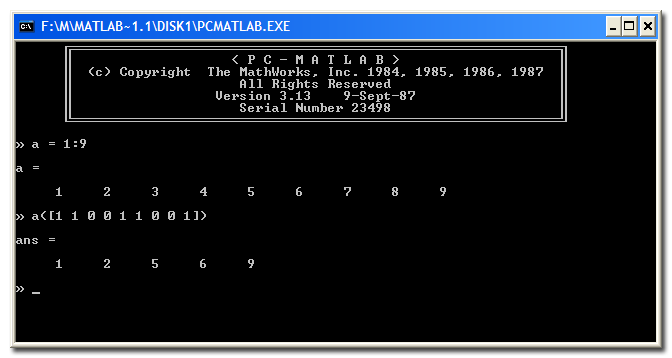
You can see above the effect of logical indexing: it extracts all the values in the locations where the indexing vector (or matrix) equals 1.
I don't know if this logical indexing behavior extends all the way back to the first commercial version of MATLAB in 1984. I do know that it's a very useful way to extract or modify sets of matrix elements corresponding to some criteria, and I use it all the time. I teach logical indexing when I give presentations on image processing in MATLAB.
But the logical indexing behavior implemented in these early MATLAB versions had a hidden dark side. Consider, for example, the expression A([1 1]) where A is a row vector. In early MATLAB, the result would be a two-element vector containing two copies of the first element of the vector. Unless ... the vector happened to have exactly two elements! In that case, the expression A([1 1]) would be treated as a logical indexing expression, and the output would be the same as A.
Here's a screen shot of MATLAB 4.2c (1994) showing the effect.
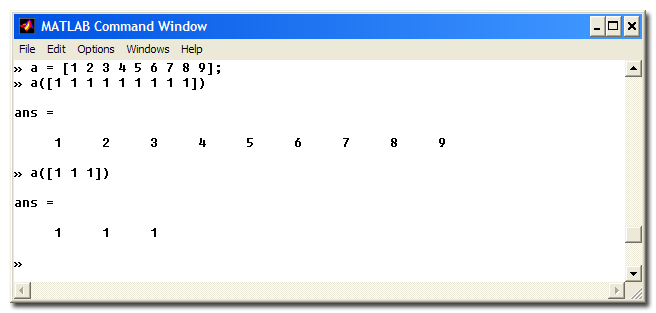
In other words, for a row vector A, A(ones(1,P)) resulted in a P-element row vector containing copies of A(1), unless A happened to have exactly P elements! Oh, that was bad. It was a bug waiting to happen in a lot of code.
We took steps to eliminate that "behavior discontinuity" in MATLAB 5.0 in 1997 by introducing the notion of a logical "attribute" of arrays. Logical operators and many appropriate functions produced outputs that were marked as logical, and only index arrays that had this logical attribute would cause logical indexing to be used.
Here's a screen shot from MATLAB 5.1 in 1997 showing this new form of logical indexing.

Notice the output of whos (there was no Workspace Browser yet). The variable b, which was the result of the expression a > 5, is shown as a double-precision matrix that is marked as logical.
This was an improvement in behavior, but there was still an issue of memory use. Double-precision is quite a "heavy" data type to be using for binary values! Nondouble data types had just been introduced in MATLAB 5.0, but hardly anyone knew about it yet. Only the Image Processing Toolbox was taking advantage of nondouble data types then. It was at this time that the Image Processing Toolbox established its convention of treating logical matrices as binary images. Before that, matrices containing only 0s and 1s were assumed to be binary, a flawed convention that was subject to a similar ambiguity as the previous form of logical indexing.
The last big change was in MATLAB 6.5 in 2002. In this version of MATLAB, logical because its own type rather than just an attribute. Here's a screen shot showing just the Command Window and the Workspace Browser.
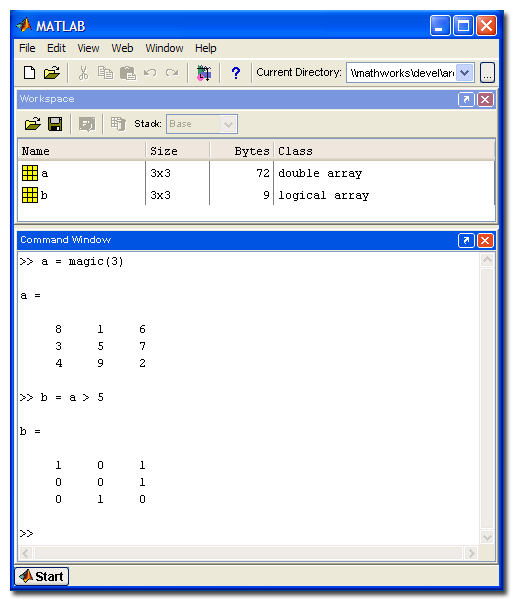
Note how the variable b has class logical instead of double, and note how it only uses 9 bytes instead of 72.
I'll wrap up today with an almost-relevant question for you: What was your first version of MATLAB, and why did you start using it? Prove that you are a power reader and got to the end of this blog entry by posting your answer as a comment below.









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.