Making Color Spectrum Plots – Part 3
Recently, I've been explaining how I made this plot, which is from DIPUM3E (Digital Image Processing Using MATLAB, 3rd ed.):
In my July 20 post, I showed one way to compute the spectral colors to display below the x-axis. Today I'll finish up by explaining the use of the colorbar function. These techniques are used in the DIPUM3E functions spectrumBar and spectrumColors, which are available to you in MATLAB Color Tools on the File Exchange and on GitHub. The entire set of DIPUM3E functions is also on GitHub.
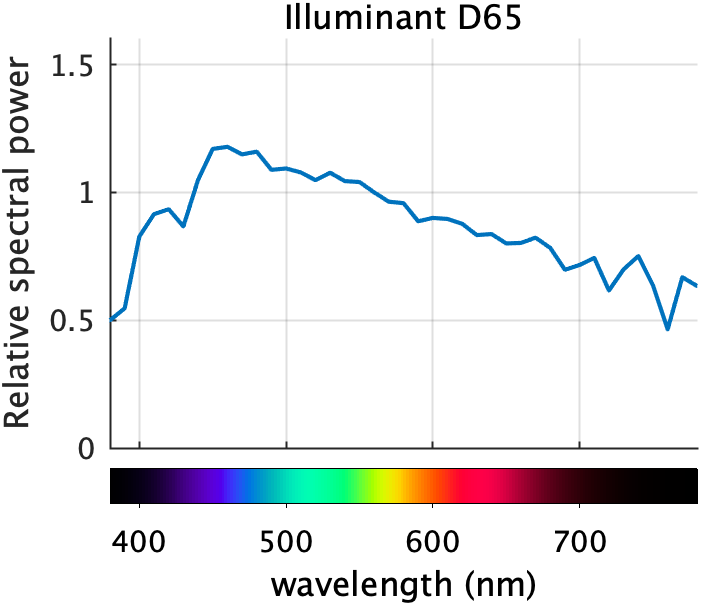
Let's just start with a plot and a colorbar with the default settings.
T = illuminant("D65"); plot(T.lambda,T.S) xlabel('wavelength (nm)') ylabel('Relative spectral power') title('Illuminant D65') grid on xlim([380 780]) cb = colorbar
cb =
ColorBar with properties:
Location: 'eastoutside'
Limits: [0 1]
FontSize: 9
Position: [0.8482 0.1095 0.0286 0.8167]
Units: 'normalized'
Use GET to show all properties

Well, let's fix the colors first. The colorbar automatically picks up its colors from the axes Colormap property, if it is set, or from the figure Colormap property. I'll set it on the axes. I also need to set the CLim property to establish the relationship between the colormap colors and the spectrum wavelength values.
[colors,lambda] = spectrumColors; ax = gca; ax.Colormap = colors; ax.CLim = [min(lambda) max(lambda)];
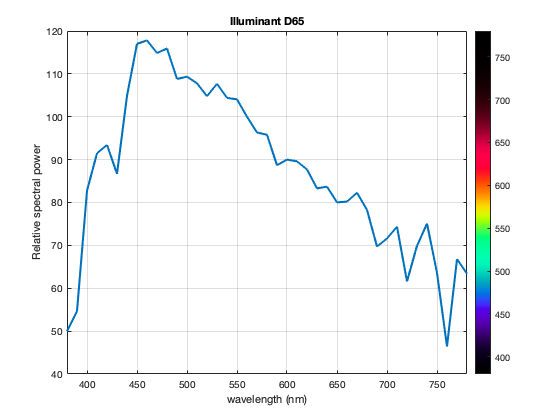
Now let's get it in the right place.
cb.Location = 'southoutside';
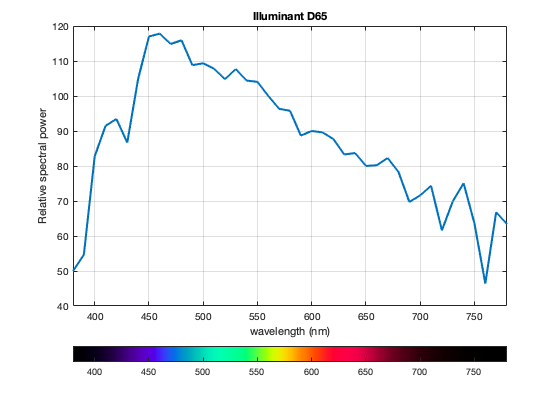
The final tweaks set things up so that the x-axis labels appear under the colorbar.
cb.Ticks = ax.XTick;
cb.Label.String = ax.XLabel.String;
cb.TickDirection = "out";
ax.XTickLabels = [];
ax.XLabel = [];

There you go. This nontraditional use of colorbar works pretty well as an auxiliary color label for the x-axis (or y-axis). If you find another use for this technique, let us know in the comments.








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.