Random Number Generators, Mersenne Twister
This is the first of a multi-part series about the MATLAB random number generators.
Contents
Taking control
If you issue the following commands at any point in any recent version of MATLAB, you will always get this plot.
rng default
hist(randn(10000,1),100)
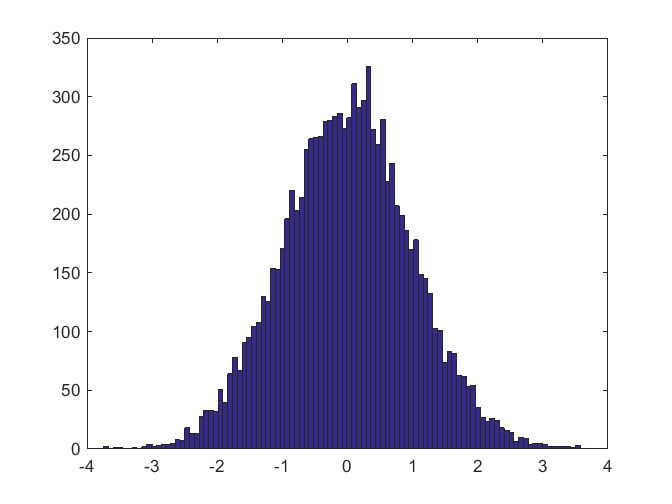
The rng command controls the random number generator that is used by the rand, randn, and randi functions. When called with the default parameter, rng resets the generator to the condition that it has when a fresh MATLAB is started. To see what that condition is, just call rng by itself.
rng
ans =
Type: 'twister'
Seed: 0
State: [625x1 uint32]
We see that the default generator is 'twister', the default seed is 0, and that the state is a length 625 vector of unsigned 32-bit integers.
If you ask for help rng, you will get lots of information, including the fact that there are three modern generators.
Generator Description ------------------------------------------------------ 'twister' Mersenne Twister 'combRecursive' Combined Multiple Recursive 'multFibonacci' Multiplicative Lagged Fibonacci
The remainder of today's post is about 'twister'. I will cover the others in future posts.
Mersenne Twister
Mersenne Twister is, by far, today's most popular pseudorandom number generator. It is used by every widely distributed mathematical software package. It has been available as an option in MATLAB since it was invented and has been the default for almost a decade.
Mersenne Twister was developed by professors Makoto Matsumoto and Takuji Nishimura of Hiroshima University almost twenty years ago. Here is their home page. The C source code is available here.
Mersenne primes
Mersenne primes are primes of the form 2^p - 1 where p itself is prime. They are named after a French friar who studied them in the early 17th century. We learn from Wikipedia that the largest known prime number is the Mersenne prime with p equal to 57,885,161. The Mersenne Twister has p equal to 19937. This is tiny as far as Mersenne primes go, but huge as far as random number generators are concerned.
Why the name?
Matsumoto explains how the name "Mersenne Twister" originated in the Mersenne Twister Home Page.
MT was firstly named "Primitive Twisted Generalized Feedback Shift Register Sequence" by a historical reason. Makoto: Prof. Knuth said in his letter "the name is mouthful." Takuji: ........ a few days later Makoto: Hi, Takkun, How about "Mersenne Twister?" Since it uses Mersenne primes, and it shows that it has its ancestor Twisted GFSR. Takuji: Well. Makoto: It sounds like a jet coaster, so it sounds quite fast, easy to remember and easy to pronounce. Moreover, although it is a secret, it hides in its name the initials of the inventors. Takuji: ....... Makoto: Come on, let's go with MT! Takuji: ....well, affirmative. Later, we got a letter from Prof. Knuth saying "it sounds a nice name." :-)
Algorithm
The integer portion of the Mersenne twister algorithm does not involve any arithmetic in the sense of addition, subtraction, multiplication or division. All the operations are shifts, and's, or's, and xor's.
All the elements of the state, except the last, are unsigned 32 bit random integers that form a cache which is carefully generated upon startup. This generation is triggered by a seed, a single integer that initiates the whole process.
The last element of the state is a pointer into the cache. Each request for a random integer causes an element to be withdrawn from the cache and the pointer incremented. The element is "tempered" with additional logical operations to improve the randomness. When the pointer reaches the end of the cache, the cache is refilled with another 623 elements.
The algorithm is analyzed by investigating the group theoretic properties of the permutation and tempering operations. The parameters have been chosen so that the period is the Mersenne prime 2^19937-1. This period is much longer than any other random number generator proposed before or since and is one of the reasons for MT's popularity.
By design, the results generated satisfy an equidistribution property in a 623-dimensional cube.
Doubles
Here is the function in the Mersenne Twister source code that converts a pair of random uint32s into a random double. You can see that it takes the top 27 bits of one int and the top 26 bits of the other, sticks them together, and multiplies by what MATLAB would call eps/2. This is the only place in the code where floating point arithmetic is involved.
double genrand_res53(void)
{
unsigned long a=genrand_int32()>>5, b=genrand_int32()>>6;
return(a*67108864.0+b)*(1.0/9007199254740992.0);
}The result would be zero in the highly unlikely event that both a and b are zero. If that happens, the MATLAB interface rejects the result and calls this function again. So the smallest double results when a equals zero and b equals 1. The largest double results when both a and b are all 1's. Consequently, the output from rand is in the closed interval
$$ 2^{-53} \leq x \leq 1-2^{-53} $$
Seeds, Streams and State
For more about random number seeds, streams, and state, see Peter Perkins, guest blogger in Loren's blog. And, of course, see the documentation.
Thanks
Thanks to Peter Perkins for the work he has done on our random number suite over the years, and for enlightening me.
References
M. Matsumoto and T. Nishimura. "Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudorandom Number Generator." ACM Transactions on Modeling and Computer Simulation, 8(1):3-30. 1998. Available online at: <http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/ARTICLES/mt.pdf>.







コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。