
The Closest Pair of Points problem is a standard topic in an algorithms course today, but when I taught such a course fifty years ago, the algorithm was not yet known.... read more >>

The Closest Pair of Points problem is a standard topic in an algorithms course today, but when I taught such a course fifty years ago, the algorithm was not yet known.... read more >>

I have spent much of my career working to bring abstract linear algebra and practical matrix computation closer together. This project is my latest effort.... read more >>
(I have a guest blogger today. Ron Jones worked with me in 1985 for his Ph. D. from the University of New Mexico. He retired recently after nearly 40 years at Sandia National Labs in Albuquerque and now has a chance to return to the problem he studied in his thesis. -- CBM)... read more >>

When I tackle a Wordle puzzle, I like to make all the key decisions myself. My three assistants set up puzzles and suggest words when I ask for help, but I guide the actual solution. My assistants also make it possible for me to play Wordle anywhere, anytime, even when my laptop is in airplane mode. I don't need the New York Times or access to the Web.... read more >>
(The January 5 posting was premature and incomplete.)... read more >>

Quaternions are generalizations of the complex numbers that have found applications in computer graphics and many other fields.... read more >>

I am giving a five-minute talk today, May 26, at the virtual seminar on Complexity of Matrix Computations. Here are my slides. Two new MATLAB functions, tred and imtql, instrumented to count flops, are available in symeig.m.... read more >>
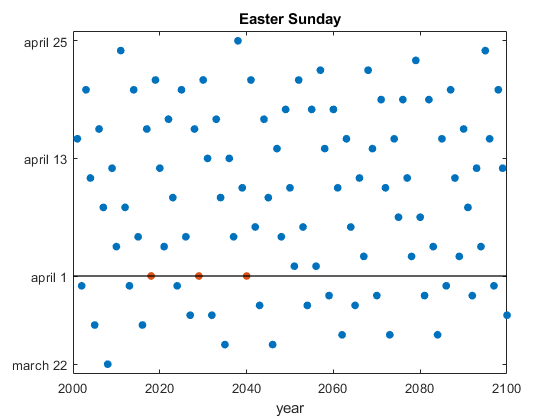
What do the years 2018, 2029 and 2040 have in common? They are the only years in the 21st century when Easter Sunday occurs on April Fools Day.... read more >>

Recently, I had email from a student in Italy.... read more >>

This post is by my colleague Cosmin Ionita.... read more >>