IBM Hexadecimal Floating Point
Our technical support group recently received a request for a tool that would convert IBM System/360 hexadecimal floating point numbers to the IEEE-754 format. I am probably the only one left at MathWorks that actually used IBM mainframe computers. I thought we had seen the last of hexadecimal arithmetic years ago. But, it turns out that the hexadecimal floating point format is alive and well.
Contents
IBM System/360
The System/360 is a family of mainframe computers that IBM introduced in 1965 and that dominated the computer industry until PCs came along twenty years later. They range in size from desk-sized to systems that fill a large room.
Here is a photo of a mid-sized model.

System/360, Model 60. Photo from Ken Shirrif's blog, IBM 360/System Summary.
The System/360 architecture is byte-oriented, so it can handle business data processing as well as scientific and engineering computation. This leads to base-16, rather than base-2 or base-10, floating point arithmetic.
* Binary f*2^e 1/2<=f<1 * Decimal f*10^e 1/10<=f<1 * Hexadecimal f*16^e 1/16<=f<1
Formats
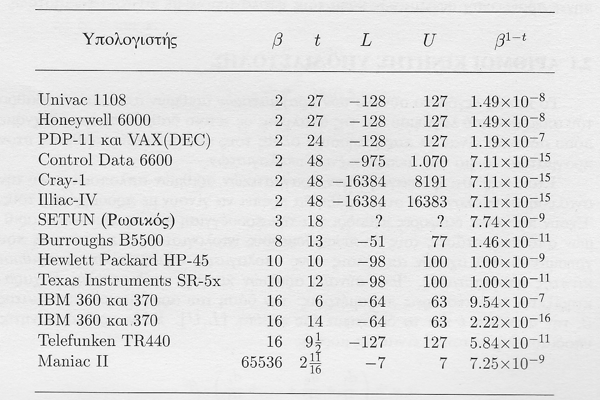
Floating point formats played an important role in technical computing in the early days. This table from FMM lists formats that were in use in the 1970s, before IEEE-754 was introduced in 1985.

Data
The System/360 hexadecimal format is used in many industries for the preservation of data files.
CREWES. Teaching exploration seismology. Comprehensive MATLAB toolbox for use with the textbook "Numerical Methods of Exploration Seismology with algorithms in Matlab" by Gary F. Margrave, a geoscience professor at the University of Calgary.
Library of Congress. Government.
NASA. Astronautics.
SAS. Statistics and business analytics. SAS wrapers for C.
Enthought. Python wrappers for C.
Hex_ieee
Hex_ieee. I have two twenty-line MATLAB functions, ieee2ibm and ibm2ieee, that convert IEEE-754 floating point to and from IBM hexadecimal format.
Three statements in the middle of ieee2ibm are the key to the entire operation. The first statement is
[~,e] = log2(x)
With two output arguments, log2 returns the mantissa and exponent of an IEEE-754 floating point number. The mantissa is not needed here.
The second key statement
e = ceil(e/4)
makes e divisible by 4. This turns e into the appropriate hexadecimal exponent so that the third statement
f = x.*16.^(-e)
can produce the hexadecimal mantissa.
ieee2ibm
function z = ieee2ibm(x)
Convert IEEE-754 to IBM System 360 hexadecimal.
z = ieee2ibm(x)
Input x, real column vector.
Output z, length(x)-by-16 char.
Example: ieee2ibm(-118.625) = 'C276A00000000000'.
s = sign(x); % -1, 0, or 1
x = abs(x);
x(x < 16^(-65)) = 0; % Underflow
x(x >= 16^63) = (1-eps/2)*16^63; % Overflow
[~,e] = log2(x); % base 2 exponent
e = ceil(e/4) % base 16 exponent
f = x.*16.^(-e); % base 16 mantissa
E = uint64((e+64)*2^56); % Assemb1e output
F = uint64(f*2^56);
S = uint64((1-s)*2^62); % 1 or 0
z = dec2hex(S + E + F); % z = 'ZZFFFFFFFFFFFFFF'
end
ibm2ieee
function x = ibm2ieee(z)
Convert IBM System 360 hexadecimal to IEEE-754.
x = ibm2ieee(z)
Input z, n-by-16 char.
Output x, n-by-1 double.
Example: ibm2ieee('C276A00000000000') = -118.625.
E = hex2dec(z(:,1:2)); % Disassemble input
F1 = hex2dec(z(:,3:8)); % < 16^6
F2 = hex2dec(z(:,9:end)); % < 16^8
s = sign(128-E); % -1 or 1
e = E-(s>0)*64-(s<0)*192; % base 16 exponent
f = F1/16^6 + F2/16^14; % base 16 mantissa
x = s.*f.*16.^e;
end
Examples
Underflow. Anything < 16^(-65) is too small and is flushed to zero. There are no denormals.
Overflow. Anything >= 16^63 is too large. There is no inf or NaN.
* 1.0 4110000000000000 * 0.1 401999999999999A * -pi C13243F6A8885A30 * 5.3976e-79 0010000000000000 * 7.2370e+75 7FFFFFFFFFFFFFF8
Comparison
S/360 hexadecimal has 7 exponent bits, while IEEE-754 has 11. Consequently, hexadecimal has a much smaller range, 5.4e-79 to 7.2e+75 versus 2.2e-308 to 1.8e+308.
The base-16 normalization implies that hexadecimal effectively has between 53 and 56 mantissa bits. Counting the hidden bit, IEEE-754 also has 53. So, the accuracy of the two is pretty much the same.
Software
My functions ieee2ibm and ieee2ibm described above, modified to handle both single and double, plus hex_test, which does what its name implies, are available at Hex_ieee.
Homework: What happens?
ok = 0;
for k = 1:10
x = single(k/10);
ok(k) = hex_test(x);
end
ok







评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。