The Revolving Century puzzle is a beautifully made wooden puzzle from Creative Crafthouse in Hudson, Florida.... 続きを読む >>

The Revolving Century puzzle is a beautifully made wooden puzzle from Creative Crafthouse in Hudson, Florida.... 続きを読む >>
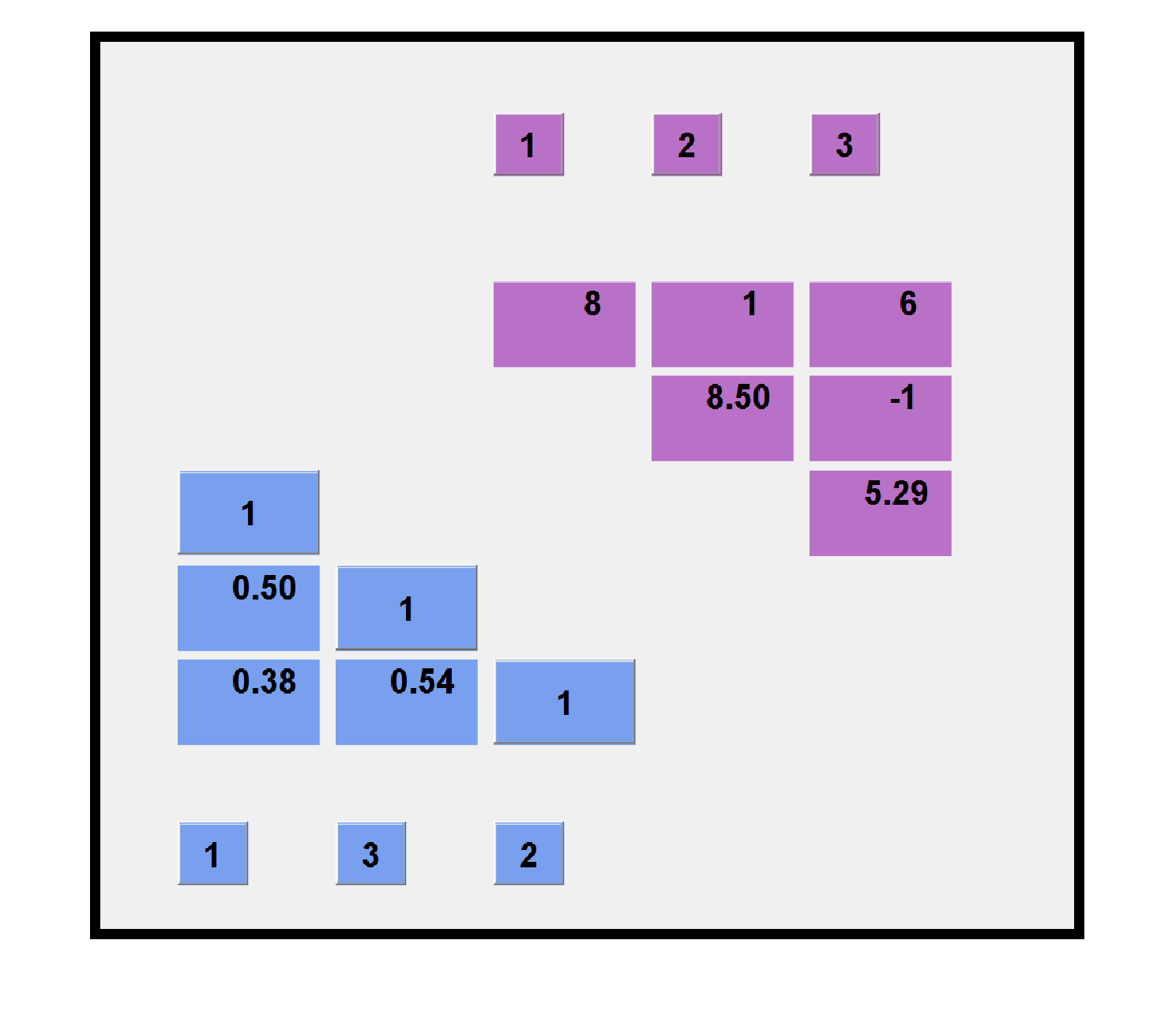
LUTool provides an interactive animation of Gaussian elimination, the most important algorithm in technical computing.... 続きを読む >>

The answer: A\A is always I, except when it isn't.... 続きを読む >>

A news story released yesterday, March 31,by c|net has the headline... 続きを読む >>

The rank of a linear transformation is a fundamental concept in linear algebra and matrix factorizations are fundamental concepts in numerical linear algebra. Gil Strang's 2020 Vision of Linear Algebra seeks to introduce these notions early in an introductory linear algebra course.... 続きを読む >>

I want to share some colorful images featuring the seven colors in the MATLAB axes color order.... 続きを読む >>

My post a few days ago, Gil Strang and the CR Matrix Factorization, generated a lot of email. Here is the resulting follow-up to that post.... 続きを読む >>

My friend Gil Strang is known for his lectures from MIT course 18.06, Linear Algebra, which are available on MIT OpenCourseWare. He is now describing a new approach to the subject with a series of videos, A 2020 Vision of Linear Algebra. This vision is featured in a new book, Linear Algebra for Everyone.... 続きを読む >>

Line plots with a color order from one of our color maps are useful, and pretty.... 続きを読む >>

The floating point arithmetic format that occupies 128 bits of storage is known as binary128 or quadruple precision. This blog post describes an implementation of quadruple precision programmed entirely in the MATLAB language.... 続きを読む >>