Jiří’s Ovozoetrope
We have a treat today: a guest visit from MATLAB user and controls researcher Jiří Zemánek.

Jiří is a doctoral student at the Czech Technical University in Prague. He also likes eggs. But first, consider this spiral pattern.

Now spin it around. At this rate of rotation, your eye follows the spinning pattern as a whole. Like any image on a turn table, it’s just turning in place.

But if we spin it somewhat faster (that is, rotate it through a larger angle between frames), something interesting happens. The dots now move in such a way that it looks like an animation of individual dots moving on their own. Blue dots are being sprayed from the center in a sprinkler pattern. It’s the same pattern, but at a particular stroboscopic frequency your perception of what’s happening changes dramatically. This is the basic idea behind a zoetrope, which you may recall from a post last year.

That brings us back to Jiří. By day, Jiří builds control systems for manipulation using electric and magnetic fields (check out the awesome Magman project from a few years ago). But by night, Jiří becomes a brilliant egg-obsessed animator. Okay, that might be a slight exaggeration (orange you glad I didn’t say eggsaggeration?), but Jiří has used his MATLAB chops to design zoetrope-able patterns on the sides of eggs. To transfer the images to the egg, he used an Eggbot from Evil Mad Scientist Laboratories. Then he takes them for a spin. Rotate the eggs around at exactly the right speed (and use a strobing shutter) and the designs spring to life.
Czech out his video. I mean, check out his video (sorry, I couldn’t resist).
Amazing, huh? I call it the Ovozoetrope. Jiří calls it Eggstatic.
I asked Jiří if he could share any of his pattern-generating MATLAB code with us. He said it’s not available in a convenient form yet, but he may make an egg animation tutorial sometime soon. In the meantime, I noticed that he said he was inspired by patterns from phyllotaxis. This encouraged me to try an example of my own.
Phyllotaxis is a fancy Greek word for describing how seeds or leaves arrange themselves as they grow. You may know that the seeds in a sunflower (among other plants) are laid down along a Fermat spiral (r = √θ), with one seed dropping every 137.5 degrees. That’s the Golden Angle for you fans of Phi. This arrangement lets some very simple growth rules optimize the seed packing as the plant grows.
phi = (sqrt(5)+1)/2; golden_angle = 2*pi/phi; max_angle = 1000; theta = 1:golden_angle:max_angle; r = sqrt(theta); [x,y] = pol2cart(theta,r); plot(x,y,'.')
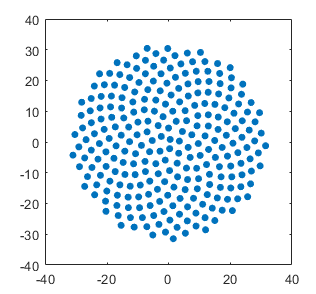
Phyllotaxis patterns are ideal for zoetropic animation. I took this pattern and animated it. The result gives you a visceral sense of how the seeds come into existence at the center of the flower and slowly radiate outward. Amazingly, there are only 11 frames in this animation.
My version is not on an egg, but it could be. The idea is the same. Maybe Jiří can do a seed-packing egg animation one of these days.
So if you celebrate Easter, then Happy Easter! If you don’t, then Happy Check-Out-These-Amazing-Zoetropic-Eggs!
- 범주:
- Maker









댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.