Best trivia question ever: What is a scutoid?
If you want to really stump your friends at trivia night, simply ask them, “What is a scutoid?” Chances are, despite being covered in them from head-to-toe, they won’t know. The truth is, no one knew until just recently, because scutoids were just discovered, and therefore just recently named.
So, what is a scutoid?
A scutoid is a three-dimensional shape that resembles a twisted column with a portion of one side cut off. The top is a pentagon, the bottom is a hexagon, and one of the “edges” resembles a “Y”, enabling the one vertex on the pentagon to connect to two vertices on the hexagon. Its unique shape enables it to pack together with other scutoids and create curved surfaces.
But why do we really care, you ask? This newly discovered shape may be the reason we exist. According to The New Yorker, “The shape, however odd, is a building block of multicellular organisms; complex life might never have emerged on Earth without it.”
It turns out that much of our bodies are comprised of cells in the shape of scutoids, from the outer layer of our heart and lungs to our epidermis. Scutoids enable our epithelial cells to form curves and bends. They are crucial to how our organs develop as cells divide.
Computer simulation discovers the new shape
It wasn’t a team of mathematicians that discovered the new shape: It was an interdisciplinary team of cellular biologists and biophysicists, as well as applied mathematicians. The scientists discovered this new shape by mathematically modeling a solution for a biological problem. The study, published in Nature Communications, is the result of collaboration between groups from Seville University, Spain and Lehigh University, USA.
As cells pack together to make surfaces, energy is expended to maintain the borders between cells. Therefore, cells organize in ways to minimize these borders. The smaller the contact, the less energy is expended. As part of their research, they developed a computer model in MATLAB to simulate how cells pack together in curved tissue to minimize their borders. The MATLAB code is available on GitHub.
The simulation showed that the borders were minimized in curved surfaces when some of the cells were in the shape of scutoids. “Where you have curvature, you have scutoids,” Javier Buceta, the researcher from Lehigh University, told The New Yorker.
It’s one thing to predict that curved surfaces are comprised of scutoid-shaped cells. It’s another to show the mathematic model is correct by identifying the scutoids in living cells. The team used confocal imaging techniques to successfully identify scutoids in developing embryos of fruit flies. The more curved the surface, the higher the concentration of scutoid-shaped cells.
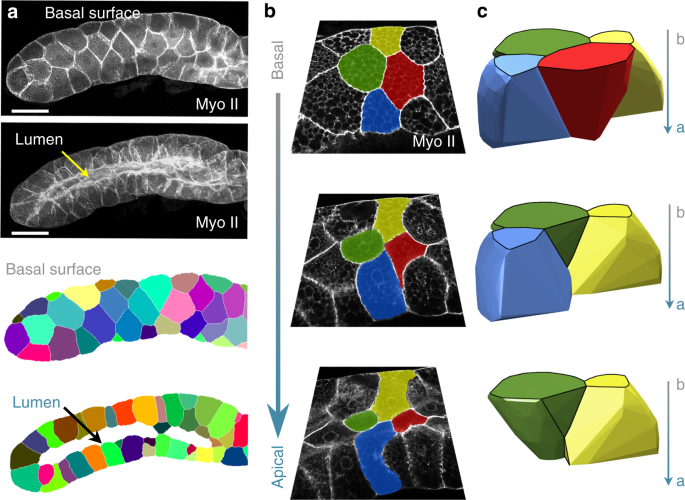
3D tissue packing of curved epithelia. The image confirms the presence of concave surfaces predicted by the mathematical model. Image credit: Nature.
Is the scutoid truly a “new” shape?
Matthew Gursky, a professor of mathematics at the University of Notre Dame, answered this very question for Popular Science. He states, ““It depends what you mean. If by ‘new’ you mean that it didn’t exist before (like a new model of car), then the answer is ‘no,’ of course. What they mean by “new” is a shape that has never been mathematically described and studied.”
So while scutoids likely existed as multicell organisms first emerged from the primordial soup, this is the first time the mathematical description of this three-dimensional object was determined and used to model how biological membranes function. So, it’s “new” to us, just as a recently discovered species is considered “new”.
What if your friend knew the answer to the trivia question?
If, by chance, your friend actually knows what a scutoid is, maybe you can trip them up with a follow-up question: “What were scutoids named after?”
The researchers asked a group of mathematicians what the shape called, only to learn it did not have a name. “When we found the shape, we said, ‘Let’s talk to the mathematicians—for sure they know the name of this,’” Buceta said. “But they couldn’t give us a name, because it didn’t have a name. We had to find one!” They decided that the shape resembled the scutellum of a beetle, so decided to combine “scutellum” with “prismatoid” to create “scutoid.”
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.