ノイズは自然界に広く存在ています。MATLAB にはデータや画像からノイズを除去するための機能がたくさんありますが、この記事では、自然に見える雲、地形、テクスチャを生成するためのノイズ生成方法をレビューします。 Flipbook Mini Hack contest の参加者も使用されているテクニックです。以下に例をいくつか紹介します。
この種の構造化ノイズには、1/fノイズ、コヒーレントノイズ、フラクタルノイズ、カラードノイズ、ピンクノイズ、fBm、ブラウニアンノイズなど、いくつかの分類があり、それぞれに独自の定義があります。この記事では、信号の強度と空間的または時間的周波数との間の数学的関係を説明する用語であるローパワーノイズと呼ぶことにします。ローパワーノイズは、丘や谷などのマクロな変動やテクスチャを加えるマイクロな変動を作成することができます。このタイプのノイズは、地震から金融市場に至るまでの自然現象にしばしば見られ、MATLAB で簡単に生成することができます。
MATLAB で 2D ローパワーノイズを生成するための 5 つのステップ
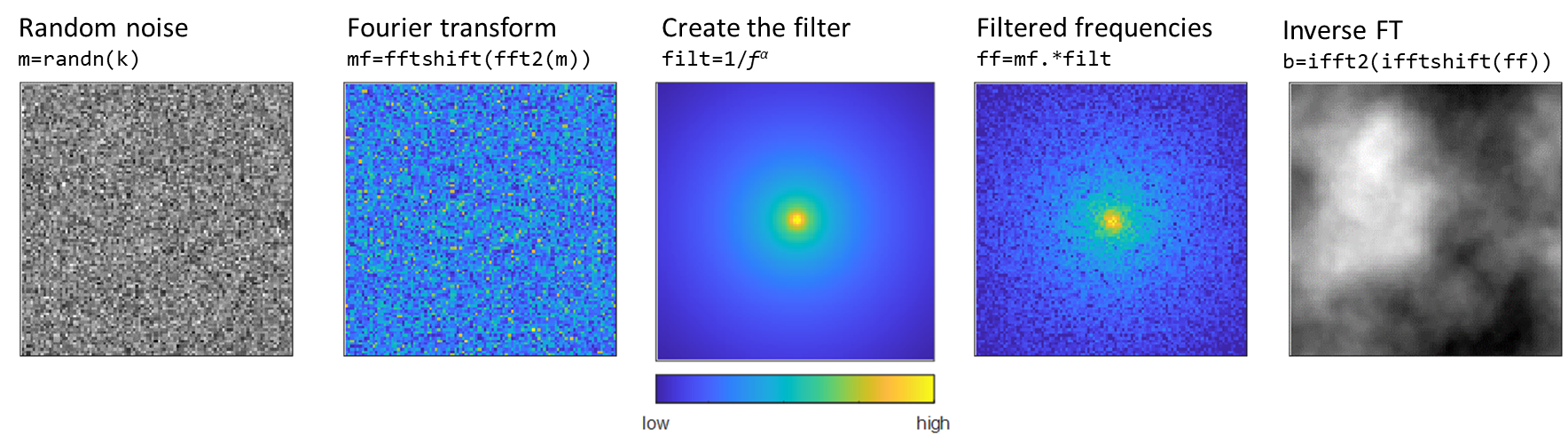
ローパワーノイズの作成は簡単で、MATLAB だと 3 つのパラメータと数行のコードです。下の画像の 5 つのステップで説明します。
ローパワーノイズを作成する 5 ステップ
1.ランダムノイズ:ランダムな値の行列を作成します。ローパワーノイズの定義の中には、randn() を使用して生成されるガウス白色ノイズから始める必要があるものもありますが、rand() を使用して生成される一様分布のランダム数値でも十分な結果が得られます。最初の 2 つのパラメータは行列のサイズとランダム数値生成器のシード(および生成器のタイプ)です。ローパワーノイズは初期値に大きく影響されるため、各シードと行列のサイズは異なる結果を生成します。サイズ k は偶数である必要があります。
rng(0,‘twister’) % Parameter 1. random number generator seed
k = 100; % Parameter 2. size of the square matrix, must be an even scalar
m = randn(k); % k-by-k matrix
2. フーリエ変換:2次元高速フーリエ変換関数 fft2() を使用して、2次元配列を空間領域から周波数領域に変換します。これにより、低周波数の係数が行列の端に、高周波数の係数が行列の中央に配置されたピラミッド状の周波数係数の行列が返されます。ステップ 4 では、この配置を反転させ、低周波数の係数が中央に、高周波数の係数が行列の端に配置されるようにする必要があります。配置を反転させるには fftshift() を使用します。
2次元の周波数係数をどう解釈するのでしょうか?この段落は興味をもってくれた読者と、簡潔に説明する私の個人的な挑戦のためのものです。2次元フーリエ変換は、画像を様々な周波数と向きを持つ平面的な正弦波に分解します。周波数係数は複素数であり、平面波を組み合わせたり重ね合わせたりして画像を再現するための一連の指示を提供します。mf(u,v) の値を考えてみましょう。mf(u,v) の実部と虚部は、行 u と列 v に割り当てられた周波数によって定義される2次元正弦波平面の振幅と位相に対応します。MATLAB の画像関連の関数は複素数値をサポートしていないため、周波数係数の大きさが上記の概要図の 2 つ目と 4 つ目で表示されています。複素数の大きさは abs() を使用して計算されます。
3. フィルターの作成:ローパワーノイズの重要な特徴は、低周波数の支配性と、変動に寄与する高周波数。これにより、2次元の丘や雲のようなマクロなパターンを画像に作り出しつつ、テクスチャを加えるマイクロな変動を可能にします。周波数の観点からは、細かいディテールを持つ画像の部分は高い空間周波数を持ち、より滑らかな部分は低い空間周波数を持ちます。フィルターの目的は、画像の低い空間周波数を強調してマクロなパターンを作り出すことです。ステップ 2 でシフトされたフーリエ変換行列 mf は、低周波数の係数が中心に配置されていることを思い出してください。したがって、2次元フィルターは周波数に対して逆の関係($ 1/f$ ここで、2次元信号の場合は $f = \sqrt{f_u^2 + f_v^2}$)を持つべきであり、中心の低周波数にはより大きな重みを置き、周囲の高周波数にはより少ない重みを置くようにします。低周波数をどの程度重視するかは第 3 のパラメータ、$1/f^α$ の指数によって制御され、通常は 0<α<=3 の範囲内に納めます。α の値が大きいほど、低周波数からの影響が大きくなり、以下の画像に示されるように、詳細なテクスチャが少ない結果となります。αの値は、白色ノイズ(α=0)、ピンクノイズ(α=1)、ブラウニアンノイズ(α=2)など、ノイズのいくつかの分類を定義するために使用されます。
係数の影響を確認:大きいほど低周波数からの影響が大きくなります
これまで見たローパワーノイズの実装は、それぞれフィルターの作成方法が異なりますが、重みの分布パターンは同じです。このフィルターはステップ 5 で実数値を返し非常に堅牢ですが、k が偶数である必要があります。
a = 2; % Parameter 3. 1/fᵅ exponent
filt = dd .^ -a; % frequency filter
filt(isinf(filt))=1; % replace +/-inf at DC or zero-frequency component
4. フィルターされた周波数:シフトされたフーリエ変換行列にフィルターを掛けます。通常、座標 (u,v) の値が画像の(u,v) のピクセルの強度を決定すると考えがちなので、5 ステップのまとめの4つ目の画像を見ただけでは、この行列が最終的な画像にどのように寄与するかを想像するのは難しいと思います。この画像では、行列の中央ほど高い値の係数を持つので、これは低い空間周波数が最終結果により大きな影響を与えること想像できます。
5. 逆フーリエ変換:ランダムな値の行列から始めて、フーリエ変換はランダム行列を周波数領域で再構築し、フィルターで低周波数を強調しました。最後のステップは、フィルターされた周波数を空間領域に戻すことです。ifftshift() を使用して周波数を元のピラミッド状の配置に戻し、低周波数の係数を端に、高周波数の係数を中央に配置します。その後、2次元逆フーリエ変換をifft2() を使用して適用します。
b = ifft2(ifftshift(ff));
結果として得られた b は、元の画像と同じサイズの構造化ノイズを形成する実数行列です。5 ステップの 5 つ目の画像に示されている結果をimagesc(b) を使用して表示し、カラーバーを適用して画像の強度値を確認します。
ノイズ値を[-1,1]の範囲にスケールすることは一般的であり、追加のスケーリングを適用するのが容易になります。結果をスケールするには rescale() を使用します。
bScaled = rescale(b,-1,1);
フーリエ変換された画像にフィルターを適用し、そのプロセスを画像に逆戻しするというこのパターンは画像処理で一般的であり、画像フィルターについて学ぶ良い課題となります。
ローパワーノイズ行列の可視化
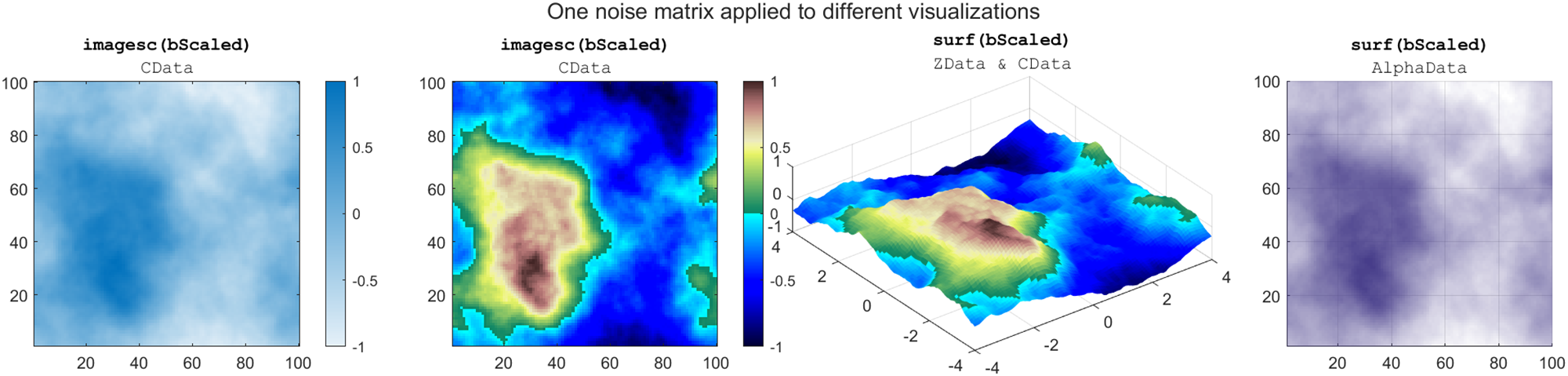
ローパワーノイズ値の配列は、カラーデータやアルファ値(透明度)または3次元平面の高さにも適用できます。以下の図は、同じノイズ行列を 4 つの異なる方法で可視化したものです。
同じローパワーノイズ行列の異なる可視化
これらは上記で紹介した 5 ステップに従ってローパワーノイズ行列(
bScaled)を作成しますが、サイズパラメータを
k=500 に置き換えてください。その後、以下のコードを続けます。2つ目、3つ目はこの記事に添付されているカスタムカラーマップ
terrainmap を使用しています(
download)。Mapping Toolboxには、改良された地形カラーマップ、
demcmap があるので使えるかもしれません。
colormap(gca,terrainmap()) % custom colormap
x = linspace(-4, 4, width(bScaled));
y = linspace(-4, 4, height(bScaled));
surf(x,y,bScaled,EdgeColor=‘none’)
colormap(gca,terrainmap()) % custom colormap
s = surf(zeros(k,k),FaceColor=[.28 .24 .54],EdgeColor=‘none’,…
AlphaData=bScaled,FaceAlpha=‘flat’);
テクスチャを強調するための光の使用
ローパワーノイズによって提供されるテクスチャは、グラフィックスオブジェクトの色の変化が十分でないと見過ごされてしまいます。MATLAB での照明の使用は、オブジェクトに詳細な陰影を加えることでテクスチャを強調することができます。以下の画像は、上の曲面プロットと同じ山を示しています。水位は、別のノイズ行列によって定義された色の平面として追加しました。光の位置は、
cameratoolbar ツールを使用して手動で選択し、再現性のために以下のコードに値だけ取り出しています。カメラのプロパティは、山にズームインするように設定しています。
ライティングでテクスチャを強調
rng(0,‘twister’)
k = 500;
mountainHeights = makenoise(k, 2); % mountain noise
figure()
x = linspace(-4, 4, k);
y = linspace(-4, 4, k);
mountainHeights = mountainHeights + 0.3; % raise the mountain
surf(x,y,mountainHeights,EdgeColor=‘none’)
colormap(flipud(copper))
hold on
seaShading = makenoise(k, 1.5); % water color noise
nColors = 500; % number of colors to use for the water
seaColors = parula(nColors*3/2);
seaColors(nColors+1:end,:) = []; % Capture the blue-green end of parula
% convert seaShading (-1:1) to colormap indices (1:500)
seaShadingIdx = round((seaShading+1)*(nColors/2-.5)+1);
% Create mxnx3 matrix of CData
cdata = reshape(seaColors(seaShadingIdx,:),nColors,nColors,3);
S=surf(x*3, y*3, 0*seaShading,CData=cdata,EdgeColor=‘none’);
axis equal off
clim([-0.5, 1.5])
light(Position = [-.8 .1 .75]) % add lighting
material dull
camva(10) % camera viewing angle
campos([-14 7 4]) % camera position
camtarget([.4 .8 .4]) % camera target
function noise = makenoise(k, a)
% Create the noise matrix
% k is the matrix size (scalar)
% a is the positive exponent (scalar)
% noise are noise values with range [-1,1]
m = randn(k);
mf = fftshift(fft2(m));
d = ((1:k)-(k/2)-1).^2;
dd = sqrt(d(:) + d(:)’);
filt = dd .^ -a;
filt(isinf(filt))=1;
ff = mf .* filt;
b = ifft2(ifftshift(ff));
noise = rescale(b,-1,1);
end
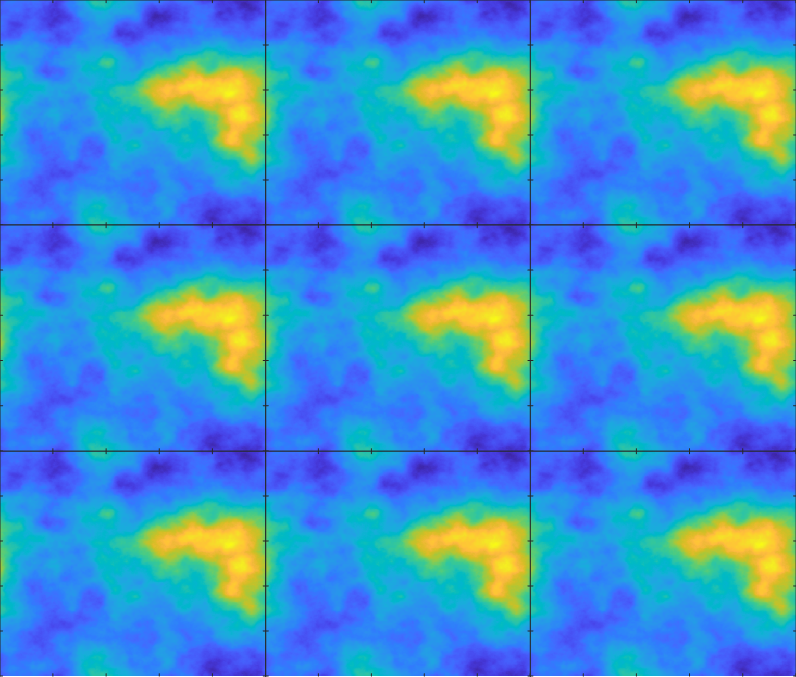
画像の結合もシームレスに
つながった画像のように配置することができる特性があります。以下は parula カラーマップを使用した行列の端がシームレスにつながっていることがわかります。
tiledlayout(3, 3, TileSpacing=‘none’, Padding=‘tight’)
set(gca,‘XTickLabel’,[],‘ytickLabel’,[])
逆に作業:指数を推定してノイズを分類する
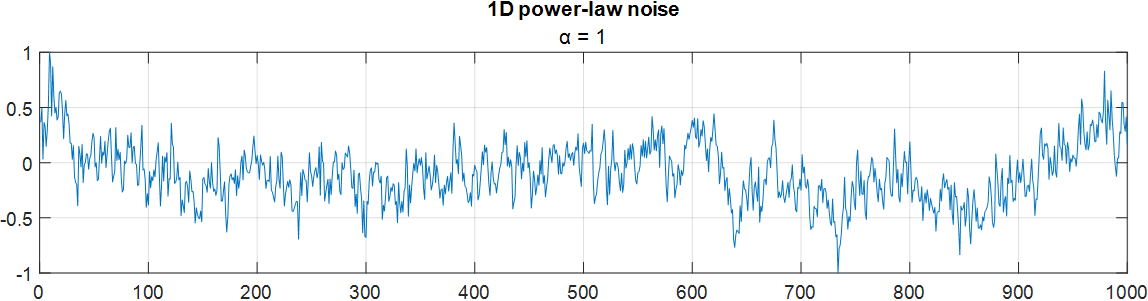
1次元(ベクトル)のローパワーノイズは、2次元の場合と同じマクロレベルの丘とマイクロレベルのテクスチャを持っています。以下は、指数 α=1 で定義されたピンクノイズの1000個の値をプロットしています。
rng default % Parameter 1. random number generator seed
k = 1000; % Parameter 2. size of the vector, must be even.
a = 1; % Parameter 3. 1/fᵅ exponent
d = sqrt(((1:k).’-(k/2)-1).^2);
filt = d .^ (-a/2); % frequency filter for 1D
ff = mf .* filt; % apply the filter
v = ifft(ifftshift(ff)); % power-law noise vector
vScaled = rescale(v,-1,1); % scaled power-law noise [-1,1]
title(‘1D power-law noise’)
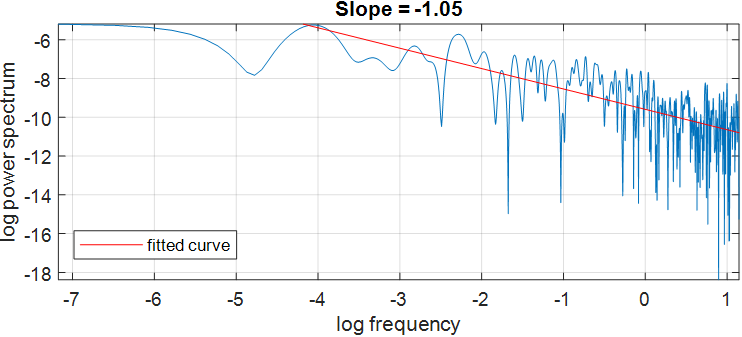
ノイズの色を分類したいとします。指数値は、log-log座標における $1/f^α$ パワースペクトルの傾きとして近似できます。MATLAB の Signal Processing Toolbox の pspectrum 関数を使ってこのタスクを簡単に行うことができます。
% Compute the power and frequency of the power-law noise vector
% Requires signal processing toolbox
[power, freq] = pspectrum(vScaled);
% Apply the log transform
infrm = isinf(freqLog) | isinf(powerLog);
% Fit the relationship between log-power and log-frequency
% Requires the Curve Fitting toolbox
F = fit(freqLog,powerLog,‘poly1’);
h.AffectAutoLimits = ‘off’;
% Print the slope in the title
ylabel(‘log power spectrum’)
title(sprintf(‘Slope = %.2f’, coeffs(1)))
近似直線の傾きは -1.05 であり、これによりこの信号はピンクノイズ(α=1)と分類されます。
まとめ
- ピンクノイズやブラウニアンノイズなどのローパワーノイズは、自然に発生するノイズを持つ2Dおよび3Dオブジェクトを作成するために使用できます。
- MATLAB でローパワーノイズ行列を作成するのは簡単(たった 5 つのステップ)
- ローパワーノイズ作成の基本原則は、ランダムの行列をフーリエ変換し、周波数係数を逆周波数で重み付けしてから逆フーリエ変換の適用。
- ローパワーノイズ行列は、色データ、アルファデータ(透明度)、高さデータ、または強度値として画像や表面に適用できます。
- 照明の使用は、表面のテクスチャを引き立たせます。
- MATLABユーザーは、2023年12月3日まで実施されたFlipbook Mini Hack contest でこの技術を使用して印象的な画像を作成しています。
追加情報
- Abhranil Das による File Exchange 上の colored_noise は、任意の次元でローパワーノイズを作成する素晴らしいツールです(git 上でも利用可能)。
- Abhranil Dasの2022年の論文 Camouflage Detection & Signal Discrimination(第5章)には、2Dフーリエ変換係数の素晴らしい解釈が含まれています。
- Paul Bourkeのノイズ生成とグラフィックスへの応用に関する 1998年の記事 はインスピレーションにあふれています。
この記事はお楽しみいただけましたか?将来の記事のコンテンツ作成に役立てるために、以下にご意見をお寄せください






댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.