物理法則を組み込んだ機械学習ってなに?
—
Physics-informed machine learning(物理インフォームド機械学習、物理法則を組み込んだ機械学習)は、Scientific Machine Learning(SciML:科学的機械学習)の一分野であり、物理法則と機械学習・深層学習を融合させたものです。この統合は双方向的であり、保存則や支配方程式、その他の専門知識といった物理の原理が AI モデルに情報を与えることで、精度や解釈性が向上します。一方で、AI は支配方程式や未知のモデルパラメータを補完・発見することができ、物理システムへの理解を深めることにもつながります。
物理インフォームド機械学習を活用することで、少ないデータでより高精度な現象予測が可能になったり、微分方程式をより効率的に解くことができます。MATLAB と Deep Learning Toolbox を使えば、物理法則を活用した AI モデルを構築し、工学や科学分野における分析や意思決定を強化することができます。このブログでは、物理インフォームド機械学習の概要として、どのような用途があるのか、物理知識とは何を意味し、それが AI にどのように情報を与えるのか、そしてこの技術の利点や有望な応用例についてご紹介します。
関連するコードやサンプルは、「SciML and Physics-Informed Machine Learning Examples」でご覧いただけます。今後の投稿では、物理インフォームド機械学習における具体的な技術についてさらに詳しく取り上げる予定です。
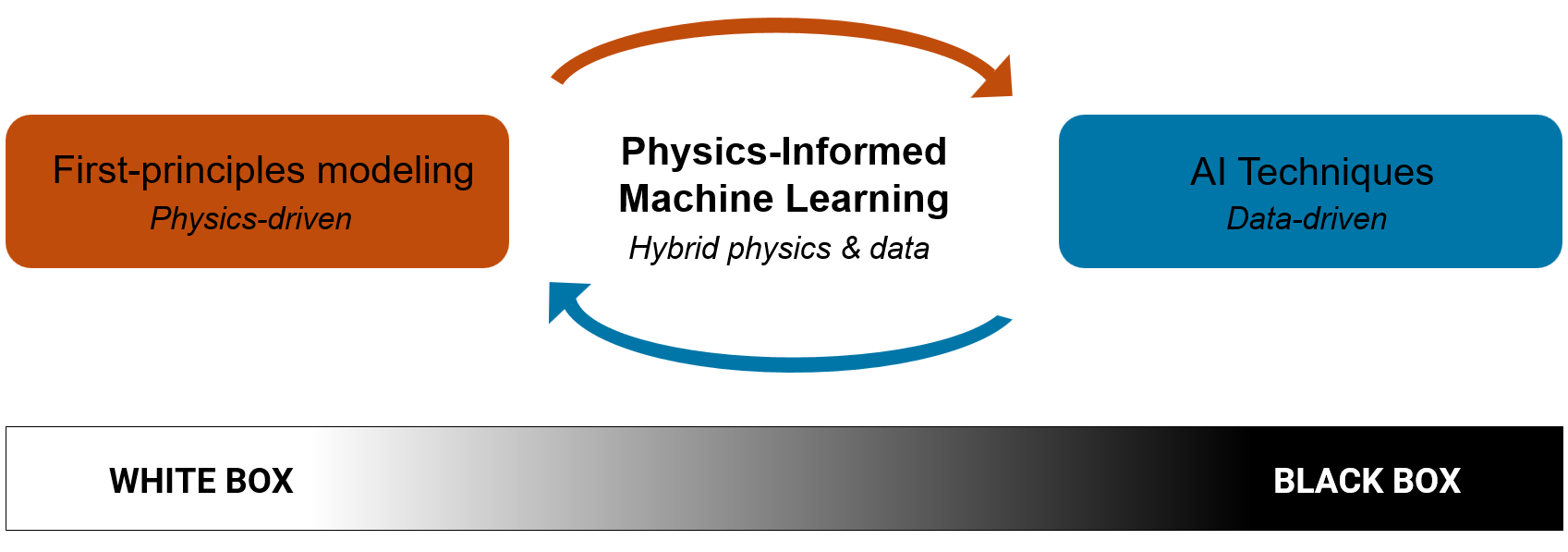
Figure: 物理インフォームド機械学習は、第一原理に基づくモデリング(ホワイトボックス)の強みと、データ駆動型 AI(ブラックボックス)の強みを組み合わせたハイブリッドアプローチです。
物理インフォームド機械学習は何に使われるのか?
物理インフォームド機械学習の多様性を説明するために、身近な例として「振り子」を使ってみましょう。下図のような振り子が揺れている様子を想像してみてください。
Figure: 単振り子のシミュレーション。このアニメーションの再現方法については、例題「振子の周期的揺れの動きのシミュレーション」をご覧ください。
次のようなことをしたいと思うかもしれません:
- データから振り子の将来の動きを予測する
- 振り子の運動を支配する根本的な方程式を発見する
- 既知の方程式を使って振り子の動きを計算する
これらのいずれのシナリオにおいても、物理インフォームド機械学習は、データと物理的知見を組み合わせるための枠組みを提供します。以下では、それぞれの目的に対して物理インフォームド機械学習がどのように応用できるかをご紹介します。
未知のダイナミクスのモデリング
振り子の角度と角速度を時間の経過とともに測定したデータがあるとします。ただし、振り子の運動を支配する正確な方程式は不明である一方で、システム全体のエネルギーが保存されることは分かっているとしましょう。
このような状況では、Hamiltonian Neural Networks(ハミルトンニューラルネットワーク)のような物理インフォームド機械学習手法を用いることで、データから学習し、エネルギー保存則を考慮しながら振り子の将来の動きを予測するモデルを構築することが可能です。
方程式の発見
今度は、振り子の運動を時間的に記述する方程式を発見したいとしましょう。SINDy(Sparse Identification of Nonlinear Dynamics)のような物理インフォームド機械学習手法を使えば、データから根本的な数理的関係を明らかにすることができます。たとえば、標準的な振り子の方程式に未モデル化の摩擦があると疑われる場合、こうした方程式発見技術を用いることで、摩擦の力学モデルを導き出すことが可能です。
既知の方程式の解法
支配方程式がすでに分かっている場合には、実験データと組み合わせて振り子の角度を時間的に予測したり、異なる条件(たとえば外力を変えるなど)で方程式を解いたりすることができます。Physics-Informed Neural Networks(PINNs)のような手法では、常微分方程式(ODE)や偏微分方程式(PDE)といった支配方程式をデータと組み合わせて、観測データと物理法則の両方に一致する解を求めることができます。さらに、異なる外力関数に対応する支配方程式の数値解がすでにある場合には、Fourier Neural Operator のようなオペレータ学習技術を使って、新しい入力(例:外力関数)に対して迅速に解(例:振り子の角度)を予測することが可能です。
以下は、振り子を用いた具体例とともに示した、3 つの異なる目的の概要です。
| 目的 | 与えられる情報 | 結果の形式 | 振り子の例 |
| 未知のダイナミクスのモデリング | 測定データ + エネルギー保存などの物理的知見 | 学習されたモデル | 振り子のデータと保存則をもとに、エネルギー保存を考慮しながら将来の動きを予測するモデルを構築する。 |
| 方程式の発見 | 測定データ + 支配方程式の項などの物理的知見 | 明示的な方程式 | 振り子のデータから、その運動を支配する方程式を発見する。 |
| 既知の方程式の解法 | 支配方程式(PINNsの場合)または入力と出力の解データ(オペレータ学習の場合) | ODE/PDEの解(PINNs)または学習された解オペレータ(オペレータ学習) | 振り子の方程式とデータを使って運動を予測する(PINNs)、または外力入力から運動を予測するモデルを学習する(オペレータ学習)。 |
Table: 物理インフォームド機械学習の主要な目的と、単振り子を用いた具体例
次回のブログ投稿では、今回紹介した物理インフォームド機械学習の具体的な手法に加え、いくつかの追加手法についても詳しく掘り下げ、MATLAB での実装方法について解説します。今回はまず、物理インフォームド機械学習における“物理”とは何か、そしてそれがどのように学習アルゴリズムに“情報を与える”のかについて探っていきましょう。
物理知識はどのように表現されるのか?
物理インフォームド機械学習では、AIモデルの設計を導いたり、制約を加えたり、着想を与えたりする形で物理的知識を表現します。振り子の例では、たとえば「系の全エネルギーが保存される(ハミルトン力学に基づく)」という知識や、「支配方程式が角加速度と位置に依存する」という知識(たとえ摩擦などの項が未知であっても)が該当します。
では、物理インフォームド機械学習の文脈において「物理知識」とは具体的に何を意味するのでしょうか?そして、その知識はAIモデルでどのように符号化(エンコード)され、活用されるのでしょうか?
物理インフォームド機械学習において、物理知識には以下のようなものが含まれます:
- 支配方程式(例:振り子の常微分方程式)
- 保存則と対称性(例:エネルギー保存)
- 境界条件および初期条件(例:初期の角度と角速度)
- ドメイン固有の知識(例:最大振れ角、周期性)
以下の表では、さまざまな種類の物理知識と、それぞれ振り子に関連する具体例を示しています。
| タイプ | 与えられる情報 | 数学表現 |
| 支配方程式 | 振り子の方程式 | \[\ddot{\theta}=\ -\omega_0^2\sin{\theta} \] |
| 保存則 | エネルギー保存 | \[E=\ \frac{1}{2}m\ell^2{\dot{\theta}}^2+mg\ell(1-\cos{\theta}) \] |
| 境界・初期条件 | 初期角度と角速度 | \[\theta\left(0\right)=\ \theta_0,\ \dot{\theta}(0)=\ {\dot{\theta}}_0 \] |
| ドメイン固有知識 | 物理制約(最大角) | \[|\theta|\le\theta_{max}\] |
Table: 振り子を用いて物理知識をどのように表現できるかの例。この一覧は網羅的ではなく、物理知識には対称性、不変性、経験則なども含まれる可能性があります。
ドメイン知識を機械学習に統合する方法とその例について詳しく知りたい方は、以下をご覧ください:Building Confidence in AI with Constrained Deep Learning、Use Physics-Inspired Estimators for Estimating Nonlinear Dynamics.
物理知識は機械学習とどのように統合されるのか?
機械学習のワークフローは通常、以下の6つのステージで構成されます:
| ステージ | 説明 |
|---|---|
| 1. 目的の定義 | モデル化すべき内容を明確にし、入力と出力の関係や既知の物理法則を特定する。 |
| 2. トレーニングデータの収集 | 実験、測定、シミュレーションなどを通じてトレーニングデータを収集し、生データを分析・モデリングに適した形式に前処理する。 |
| 3. モデルの構築 | データとタスクに最適な機械学習アルゴリズムや深層学習アーキテクチャを選択する。 |
| 4. 損失関数の定義 | 観測データとの一致や物理法則の遵守など、目的達成度を定量化する損失関数を作成する。 |
| 5. モデルの最適化 | 損失を最小化し、予測精度を高めるためにモデルのパラメータを調整する。 |
| 6. 予測の実行 | 学習済みモデルを使って予測を行ったり、システムの挙動をシミュレーションする。 |
物理はこのワークフローのさまざまな段階で組み込むことができますが、主にモデル構造(ステージ 3)と評価(ステージ 4)に情報を与える役割を果たします。また、機械学習によって得られたコンポーネントは、物理ベースのモデルを補完し、部分的に未知なダイナミクスに対応することも可能です(ステージ 1)。
物理インフォームド機械学習における重要な戦略のひとつは、物理原理に基づいた制約を課すことで、予測が正確であるだけでなく、物理的にも妥当であることを保証することです。制約の課し方には主に2 つのアプローチがあります:
- ソフト制約:物理ベースの制約を損失関数(ステージ 4)の正則化項として追加します。学習中は制約違反に対してペナルティが課されますが、学習後の予測が必ずしも制約を厳密に満たすとは限りません。
- ハード制約:モデルの構造(ステージ 3)を設計する段階で、物理的制約が常に満たされるようにします。
Deep Learning Toolbox では、これら 2 種類の物理制約(ソフト制約とハード制約)を深層学習ワークフローに組み込むためのツールが提供されており、部分的にしか分かっていない物理モデルを AI によって補完することも可能です。詳細については、ソフト制約に関する「Physics-Informed Neural Networks (PINNs) とは」およびハード制約に関するリポジトリ「AI Verification: Constrained Deep Learning」をご覧ください。
以下の表では、さまざまな種類の物理知識を機械学習モデルに統合する方法と、それぞれの制約の適用戦略、および MATLAB のコード例をまとめています。
| 物理知識 | 例 | 物理法則の挿入箇所 | コード例 |
| 支配方程式 | \[ \ddot{\theta}=\ -\omega_0^2\sin{\theta} \] | 損失関数 |
residual = dllaplacian(Theta,T,1) + omega_0^2*sin(Theta); |
| 一部不明な支配方程式 | \[ \frac{d}{dt} \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix} = \begin{bmatrix} \dot{\theta} \\ -\omega_0^2 \sin\theta + h \end{bmatrix} \] |
目的関数 |
gFcn = @(X) [X(2,:); -omega0^2*sin(X(1,:))]; gLayer = functionLayer(gFcn); |
| 保存則 | エネルギー保存 | 構造・損失関数 |
% Hamilton’s equations loss = l2loss(dq,dljacobian(H,p,1)) + l2loss(dp,-dljacobian(H,q,1)); |
| 初期・境界条件 | \[ \theta(0) = \theta_0\]
\[ \dot{\theta}(0) = \dot{\theta}_0 \] |
構造・損失関数 |
icLoss = l2loss(Theta,theta0) + l2loss(dljacobian(Theta,T0,1),thetaDot0); |
| ドメイン知識 | \[ |\theta| \leq \theta_{\text{max}} \] | 構造 |
[tanhLayer; scalingLayer(Scale=thetaMax)] |
Table: 振り子に対する物理ベースの制約の例と、それらを MATLAB を用いた深層学習モデルでどのように表現・適用できるかの例。
物理インフォームド機械学習の利点
ここまで読み進めていただいた方は、すでに物理インフォームド機械学習の実践者のような思考に近づいていると言えるでしょう!とはいえ、まだ「なぜ従来の物理ベース手法や純粋な AI ではなく、物理インフォームド機械学習を選ぶのか?」という疑問が残っているかもしれません。第一原理に基づくモデルは、解釈性や汎化性に優れていますが、計算コストが高く、すべてのシステムに適用できるわけではありません—特に物理法則が十分に理解されていない場合には限界があります。一方、AI はデータから複雑なパターンを学習し、高速な予測を行うのに優れていますが、解釈性に欠けることが多く、学習データの範囲を超えた汎化が難しい場合もあります。
物理インフォームド機械学習は、第一原理モデリングと AI を統合することで、互いの強みを活かしながらそれぞれを補完することを目指しています。とはいえ、物理インフォームド機械学習は万能な解決策ではなく、場合によっては従来の手法の方が優れていることもあります。それでも、特定の状況においては、以下のような実用的な利点を提供することができます:
- 予測精度の向上:物理的知識を取り入れることで、特にデータが限られていたりノイズが多い場合でも、予測の精度を高めることができます。
- 透明性と解釈性の向上:既知の物理法則を組み込むことで、予測がどのように、なぜ行われたのかを理解しやすくなります。
- データ効率の向上:既知の物理法則を活用することで、少ないデータでも高精度なモデルを構築することが可能になります。
- 汎化性能の向上:物理的な制約を加えることで、モデルが新しい状況にも適切に対応できるようになります。
- 推論の高速化:従来のシミュレーションと比べて、物理インフォームド機械学習モデルは迅速な予測を提供することができます。
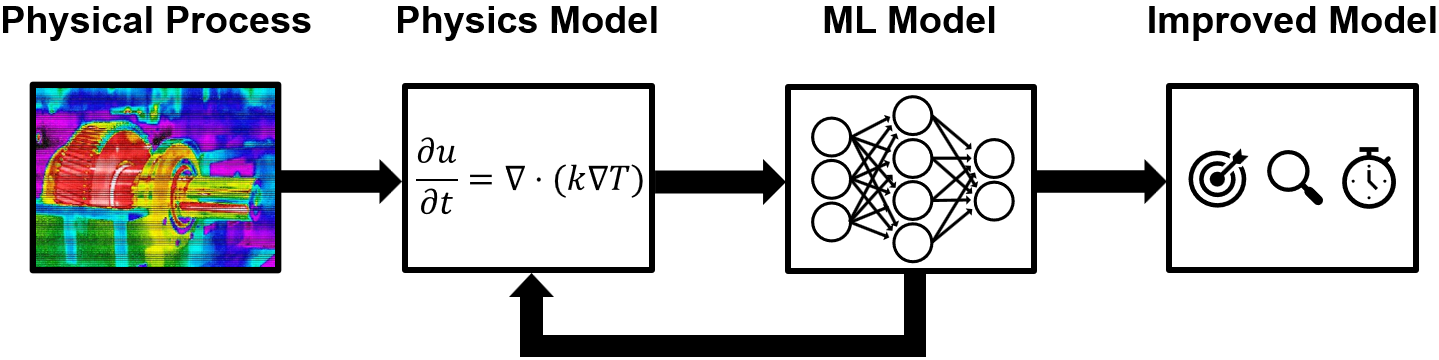
Figure: 物理インフォームド機械学習は、既知の物理法則を活用して AI モデルを強化したり、部分的にしか分かっていない物理モデルを AI によって補完・改善したりすることで、より高精度で、解釈性が高く、効率的な手法を実現します。
それでは、すでに物理インフォームド機械学習の恩恵を受けている分野をいくつか見ていきましょう。
物理インフォームド機械学習の応用例
物理インフォームド機械学習は、以下のような幅広い分野で活用されています:
- 定量的システム薬理学(QSP):
物理インフォームド機械学習モデルは、力学的な方程式と柔軟な機械学習コンポーネントを組み合わせることができ、よく理解されている生物学的プロセスとデータ駆動型の動態の両方を表現することが可能です。これらの手法は、実験データから支配方程式を特定・改良するのに役立ち、薬物の薬物動態モデルや薬物動態と薬力学の関係モデルをより正確かつ堅牢に構築することができます。
- 仮想センサー:工学分野では、熱ニューラルネットワークのような物理インフォームドモデルが、特定の熱伝達モデルの構造と、複雑または未知の効果を捉えるニューラルネットワークを組み合わせています。このハイブリッドアプローチにより、ブラックボックスモデル(例:LSTMニューラルネットワーク)よりも解釈性が高く、正確な予測が可能となり、電動モーター内の温度分布の予測など、高価な物理センサーへの依存を減らす用途に活用できます。
- PDE(偏微分方程式)シミュレーション:物理インフォームド機械学習の一部の手法は、熱伝達、流体力学、気候モデリングなどの分野で広く使われる PDE の解法に特に適しています。ある手法では、物理法則をモデルに直接組み込むことで、予測が既知の方程式と一致するようにします。また別の手法では、シミュレーションデータを活用して、異なる条件や設計におけるシステムの挙動を迅速に予測できるようにし、シミュレーションや設計探索を加速します。
データ駆動型モデリングと物理ベースのモデリングの橋渡しをすることで、物理インフォームド機械学習は、科学や工学におけるますます複雑な課題に取り組むための有力な手段となっています。
まとめ
今回の投稿では、物理インフォームド機械学習について紹介しました。これは、支配方程式や保存則といった物理的知見をAIモデルに統合することでその性能を高めると同時に、AI を活用して従来の物理ベースのモデリングを補完・拡張するという新たなパラダイムです。振り子を例に取りながら、物理インフォームド機械学習の主な目的である「データから物理システムをモデリングする」「根本的な物理方程式を発見する」「既知の微分方程式をデータの助けを借りて解く」といった応用について解説しました。
次回の投稿では、物理インフォームド機械学習の具体的な手法と、それらを MATLAB で実装する方法について、振り子の例を用いてさらに詳しく見ていきます。すぐに試してみたい方は、Scientific and Physics-Informed Machine Learning リポジトリをチェックして、コードを確認しながら実験を始めてみてください。
- Category:
- Artificial Intelligence,
- データサイエンス,
- 機能と使い方



Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.