Solving Ordinary Differential Equations
I have recently handled several help requests for solving differential equations in MATLAB. All of the cases I worked on boil down to how to transform the higher-order equation(s) given to a system of first order equations. In this post I will outline how to accomplish this task and solve the equations in question. What I am not going to talk about is details of ODE solving algorithms (maybe another time).
Contents
Simple System
Let's start with a simple, linear, second order system, a mass-spring system with motion constrained to one-dimension, a horizontal
one (and therefore no gravity). If  is the mass and
is the mass and 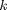 is the spring constant, the equations of motion for the system are:
is the spring constant, the equations of motion for the system are:
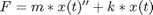
Conditions, Initial and Otherwise
To solve this system, we need to know 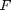 ,
,  ,
, 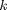 , and initial conditions, e.g.,
, and initial conditions, e.g., 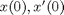 (also known as position and velocity). Let's simplify things and set
(also known as position and velocity). Let's simplify things and set 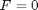 , i.e., no external forces. Let's also set some initial conditions,
, i.e., no external forces. Let's also set some initial conditions, 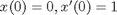 , in other words, start with the spring unstretched and the mass moving. I end up with this system:
, in other words, start with the spring unstretched and the mass moving. I end up with this system:
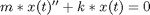
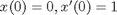
Transform Equation
Looking in the help, I need to set up an system of equations to enable me to use one of the numerical ODE solvers in MATLAB.
To start the transformation, let me define a new variable that I will substitute in the system.
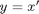
I can derive 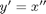
and now rewrite my ODE system in terms of 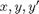 .
.
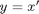
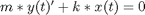
with initial conditions as above.
Now let me reorganize these 2 equations in a vector/matrix equation where 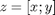
I now write me equation solely in terms of  , the new vector (consisting of position and velocity). With that in mind, I will reorganize the existing equations first
so I have
, the new vector (consisting of position and velocity). With that in mind, I will reorganize the existing equations first
so I have 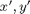 on the left-hand sides.
on the left-hand sides.
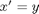
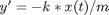
or, in terms of  ,
,
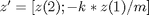
Try It!
Let's try it. Set values for m and k
m = 1; k = 10;
I can create the ODE code in a file, or I can set up the equations as an anonymous function which is what I'll do here.
springmass = @(t,z)[z(2); -k * z(1)/ m];
Set up the initial conditions.
ic = [0; 1];
Solve between 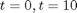 .
.
tspan = [0 10];
Call an ODE solver and plot the results.
[t,y] = ode23(springmass, tspan, ic);
plot(t,y(:,1)), title('Position vs. Time')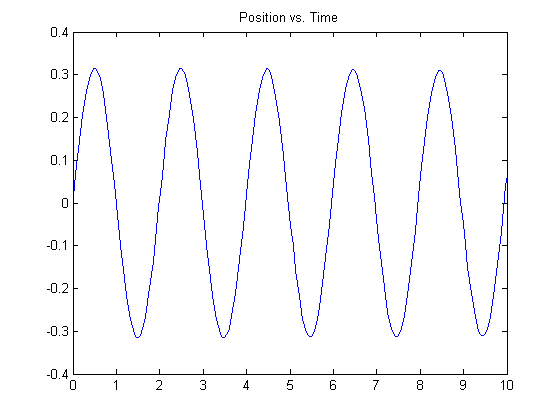
And the velocity.
plot(t,y(:,2)), title('Velocity vs. Time')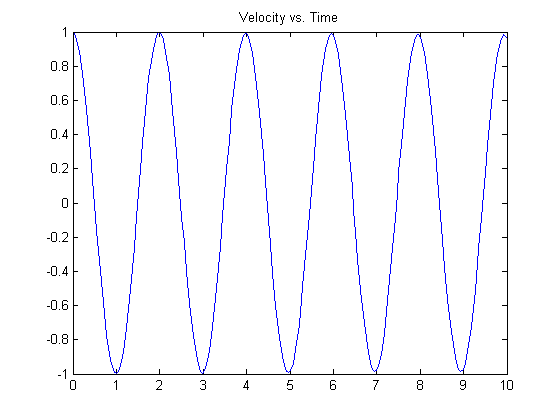
You can see the left-most points on the plots match the initial conditions specified.
Transforming Equations
Do you need to recast problems to fit into a particular formulation such as for solving ODEs? Let's hear about them here.



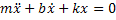





댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.