ALIKE (or not) – A Second Go At Beating Wordle
Today's guest blogger is Matt Tearle, who works on the team that creates our online training content, such as our various Onramp courses to get you started on MATLAB, Simulink, and applications. Matt has written several blog posts here in the past, usually prompted by a puzzle - and today is no different.
STUMP (v: to cause to be at a loss; baffle)
Wordle. It has captured us all. When Adam wrote his post about using MATLAB to solve Wordle puzzles, I had been thinking about doing exactly the same thing. (In the past, I have written code to cheat at Wordscapes and the NY Times Spelling Bee puzzle.) I've seen other friends post about letter distributions. I guess this is what nerds do.
When I read Adam's post, I knew I had to see if I could do better. My first thought was what reader Peter Wittenberg suggested: weighting letter probabilities by where they occurred in the word. I then tried something close to what another reader, TallBrian, suggested, by scoring words according to how much they cut down the possibilities in the next turn. I also experimented with how to choose the word with the most new letters.
But nothing worked. I couldn't make any significant improvement on Adam's 94% success rate. He had noted that there were some words in the official Wordle canon that were not in the set used to develop the algorithm. I was getting suspicious. My data-senses were tingling.
CHECK (v: to make an examination or investigation; inquire)
According to the letter probabilities, TARES is a great opening guess. But I felt like I hadn't seen too many words ending in -S, when I was playing Wordle as a human. Maybe it was time to compare the two word sets. Here I'm just repurposing Adam's code to get the two word lists. The dictionary words (called word5 in Adam's code) are in the string array trainwords. The actual Wordle list (called mystery_words in Adam's code) is in testwords.
[trainwords,testwords] = getdictionaries;
whos
The variable names show my bias: I was now thinking about this like a machine learning problem. One set of words had been used to train an algorithm - in this case, not a standard machine learning method, but a bespoke algorithm based on statistics. The other was the test set. Anyone who does machine learning knows that the quality of your model depends critically on the quality of your data. Specifically, you need your training data to accurately represent the actual data your model will be used on.
How do the letter distributions for the "training" and "test" data sets compare? First, I need to count the number of appearances of each letter in each location (for both sets of words):
% Make a list of all capital letters (A-Z)
AZ = string(char((65:90)'));
% Calculate distribution of letters
lprobTrain = letterdistribution(trainwords,AZ);
lprobTest = letterdistribution(testwords,AZ);
whos
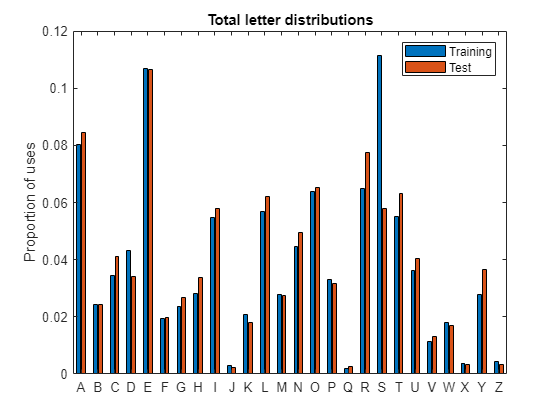
I now have two 26-by-5 matrices of the frequency of each letter of the alphabet in each position. First, let's see the overall distribution:
% Average across the 5 letter positions
distTrain = mean(lprobTrain,2);
distTest = mean(lprobTest,2);
% Plot
bar([distTrain,distTest])
xticks(1:26)
xticklabels(AZ)
xtickangle(0)
legend("Training","Test")
ylabel("Proportion of uses")
title("Total letter distributions")
Wow, something's going on with S. Sure enough, there's a big difference between the usage in the two word lists. There are also more Ds in the training set than in the actual Wordle set. Meanwhile, there are several letters that are used more in the Wordle set than the general dictionary - most notably, R, T, and Y.
Now I'm even more suspicious of words ending in -S. Let's look at the full picture of usage by letter and word location. If you do any data analysis, you will likely have encountered this situation of wanting to visualize values as a function of two discrete variables. In the past, you may have used imagesc for this, and that's certainly a reliable old workhorse. But if you don't religiously read the release notes, you may not be aware of some of the new data analysis charting functions, such as heatmap (introduced in R2017a).
heatmap(1:5,AZ,lprobTrain)
title("Letter distribution for TRAINING data")
heatmap(1:5,AZ,lprobTest)
title("Letter distribution for TEST data")
Ah, sweet vindication! Sure enough, the words we built our strategy on have a different distribution to where the common letters are used in the actual Wordle words. In particular, note that Wordle is much more likely to start a word with S than end with one. The distribution of where Es show up is different, too. To make these kinds of comparisons, it might be easier to visualize the difference between the two heatmaps:
% Take the difference in distributions
delta = lprobTrain-lprobTest;
% Find the biggest, to set the color limits symmetrically
dl = max(abs(delta(:)));
% Visualize
hm = heatmap(1:5,AZ,delta,"ColorLimits",dl*[-1 1],"Colormap",turbo);
title(["Difference in letter distribution","Red = higher prevalance in training set","Blue = higher prevalance in test set"])
Notice that I've set the color limits so that 0 is a "neutral" green, while blue or red shows a difference in either direction. The lack of -S words shows up clearly, as does the shift from -E- to -E at the end of words. Together, this suggests fewer plurals (like WORDS) and fewer -ES verb forms (eg "Adam LOVES playing Wordle") in the Wordle list.
There are a few other details in there, but they're harder to see because everything is so dominated by the difference in -S words. Let's manually narrow the color range to see more details. This will show -S as less significant than it is, but that's OK - we know about that already.
hm.ColorLimits = [-0.1 0.1];
Now we can see some interesting trends: more -Y words (presumably adjectives like "this is a SILLY topic for a blog post"), as well as more -R and -T, fewer -D words (perhaps -ED past tenses like "until Adam's post, Matt LOVED playing Wordle"), fewer instances of vowels as the second letter, and R and S switching at positions 1 & 2.
Using this heatmap, you can also see that TARES is much more aligned with the training (dictionary) set than the test (Wordle) set: every letter has a positive value in the heatmap. So while the letters are all high probability overall, this specific arrangement is particularly good for the training set and bad for the test set. A simple rearrangement to STARE reverses the situation.
ASIDE (n: a comment or discussion that does not relate directly to the main subject being discussed)
I noticed that my code jumps freely between strings, chars, and categoricals. You can see some of that in the code here, but my Wordle solver was even more liberal in its use of the different types. That might seem like evidence of bad programming - "pick a data type already!", you cry - but I'm claiming that this is actually a good practice: MATLAB gives you lots of great data types; use them! With the introduction of strings (R2016b), we get questions like "so should we just use strings now?" and "is there any point in char instead of string?". If you're confused about this, here's a simple principle: the unit of a char is a single character, the unit of a string is text of any length. Wordle is all about words... but also all about the letters! That's why it's useful to use both string (for studying words) and char (for letters).
Also, our dedicated team of developers gave us a whole pile of handy text functions along with strings. But those functions aren't just for strings - like many MATLAB functions, they accept different kinds of inputs. These ones accept text in any form and allow you to do basic text processing without regular expressions. For example, I've hypothesized that Wordle doesn't use -ES and -ED verb forms. Let's see the words that have those endings in each list:
ESDendings = @(words) words(endsWith(words,["ES","ED"]));
ESDtrain = ESDendings(trainwords)'
ESDtest = ESDendings(testwords)'
100*numel(ESDtrain)/numel(trainwords)
100*numel(ESDtest)/numel(testwords)
The handy endsWith function does what it suggests and finds the words with the given endings. Sure enough, the training data from the dictionary has many pairs of -ES and -ED verbs, like ACHED and ACHES (13.5% of the whole list). But Wordle has almost no words that are made by simply appending -ED or -ES to a 4-letter verb. Consequently, prevalence of -ED and -ES words is much lower (only 1%).
LATER (adj: coming at a subsequent time or stage)
Having confirmed that the letter distributions were indeed different, I was able to salvage my pride by building my various solution algorithms with the Wordle list and then testing them. Now I was able to successfully solve the puzzle 99% of the time. Great. But also a little unsatisfying. As any data scientist knows, training and testing with the same data set is cheating and not a good measure of how well your algorithm will perform on new data.
But... well, there is no new data. The Wordle word list is set. So it remains a valid question: given the official Wordle list, what is the best way to solve it?
Unfortunately, readers pointed out some details with what Adam had done (which I had followed). That casts doubt on my "solutions". So for now, I'll need to keep tinkering. If the New York Times haven't hidden Wordle away behind a paywall by the time I figure it out, I'll be back. I might even be brave enough to enter the internet-argument-of-the-day: what is the best starting word?
REPLY (v: to give an answer in words or writing; respond)
Adam's readers had some clever ideas on how they would go about beating this addictive game. Do any of you have a guaranteed opening word? A secret strategy that you will reveal to subscribers for only $19.95? How did you find yours and what makes it so great? Let us know in the comments.
function [word5,mystery_words] = getdictionaries
% Copied from Adam F
% read the list of words into a string array
r = readlines("https://gist.githubusercontent.com/wchargin/8927565/raw/d9783627c731268fb2935a731a618aa8e95cf465/words");
% replace diacritics using a custom function from the Appendix
rs = removediacritics(r);
% keep only the entries that start with a lower case letter
rs = rs(startsWith(rs,characterListPattern("a","z")));
% get rid of entries with apostrophes, like contractions
rs = rs(~contains(rs,"'"));
% Wordle uses all upper case letters
rs = upper(rs);
% get the list of unique five letter words
word5 = unique(rs(strlength(rs)==5));
mystery_id = "1-M0RIVVZqbeh0mZacdAsJyBrLuEmhKUhNaVAI-7pr2Y"; % taken from the sheet's URL linked above
mystery_url = sprintf("https://docs.google.com/spreadsheets/d/%s/gviz/tq?tqx=out:csv",mystery_id);
mystery_words = readlines(mystery_url);
% there's an extra set of double quotes included, so let's strip them out
mystery_words = erase(mystery_words,"""");
% also we're using upper case
mystery_words = upper(mystery_words);
end
function lprob = letterdistribution(words,AZ)
% split our words into their individual letters
letters = split(words,"");
% this also creates leading and trailing blank strings, drop them
letters = letters(:,2:end-1);
% Calculate the distribution of letters in each word position
for k = 1:5
lcount(:,k) = histcounts(categorical(letters(:,k),AZ));
end
lprob = lcount./sum(lcount); % Normalize
end
% Also from Adam
% citation: Jim Goodall, 2020. Stack Overflow, available at: https://stackoverflow.com/a/60181033
function [clean_s] = removediacritics(s)
%REMOVEDIACRITICS Removes diacritics from text.
% This function removes many common diacritics from strings, such as
% á - the acute accent
% à - the grave accent
% â - the circumflex accent
% ü - the diaeresis, or trema, or umlaut
% ñ - the tilde
% ç - the cedilla
% å - the ring, or bolle
% ø - the slash, or solidus, or virgule
% uppercase
s = regexprep(s,'(?:Á|À|Â|Ã|Ä|Å)','A');
s = regexprep(s,'(?:Æ)','AE');
s = regexprep(s,'(?:ß)','ss');
s = regexprep(s,'(?:Ç)','C');
s = regexprep(s,'(?:Ð)','D');
s = regexprep(s,'(?:É|È|Ê|Ë)','E');
s = regexprep(s,'(?:Í|Ì|Î|Ï)','I');
s = regexprep(s,'(?:Ñ)','N');
s = regexprep(s,'(?:Ó|Ò|Ô|Ö|Õ|Ø)','O');
s = regexprep(s,'(?:Œ)','OE');
s = regexprep(s,'(?:Ú|Ù|Û|Ü)','U');
s = regexprep(s,'(?:Ý|Ÿ)','Y');
% lowercase
s = regexprep(s,'(?:á|à|â|ä|ã|å)','a');
s = regexprep(s,'(?:æ)','ae');
s = regexprep(s,'(?:ç)','c');
s = regexprep(s,'(?:ð)','d');
s = regexprep(s,'(?:é|è|ê|ë)','e');
s = regexprep(s,'(?:í|ì|î|ï)','i');
s = regexprep(s,'(?:ñ)','n');
s = regexprep(s,'(?:ó|ò|ô|ö|õ|ø)','o');
s = regexprep(s,'(?:œ)','oe');
s = regexprep(s,'(?:ú|ù|ü|û)','u');
s = regexprep(s,'(?:ý|ÿ)','y');
% return cleaned string
clean_s = s;
end
- カテゴリ:
- Fun,
- Machine learning,
- Text












コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。