Minor Time Step Logging
Will's picks this week is Minor Time Step Logging by Guy Rouleau.
What actually happens when you push that Play button within Simulink? How does Simulink go about solving your system? How do you troubleshoot when the algorithm is seemingly correct, and yet your results seem dubious?
I remember these thoughts percolating in my mind when I first began developing Simulink models. If you're curious about such things, a great place to start is to read the documentation on Simulating Dynamic Systems. Amongst a treasure trove of useful information, you'll discover that one of the key concepts of Simulink is major versus minor step. Once your simulation is complete, Simulink provides the results at specific points in time. These are results on the major time step. When using a Variable-step solver, results are accurate to the error tolerances you defined in Configuration Parameters.
What's not ordinarily presented to you are Simulink's intermediary calculations as it solves your system at each major step. For certain continuous time models, minor steps aid in convergence on a solution to the equations in your model. Anyone who's taken a numerical methods class will be familiar with this concept and has probably heard of Runge-Kutta solvers, one of many solver algorithms available within Simulink.
Nine times out of ten, you won't have to worry about what Simulink is calculating on a minor step. However, having this information can prove invaluable for debugging purposes, and it can aid in the age old question, "which solver should I choose for my problem?" There are various ways of getting access to minor step values, but I absolutely love the solution Guy has provided.
All you do is drag the Minor Time Step Logging block from the library into your model and connect it to the signal of interest. Run your simulation, and voila, you have a MATLAB figure displaying the major and minor step values. I tried it on numerous models with single and multidimensional signals...worked like a charm every time.
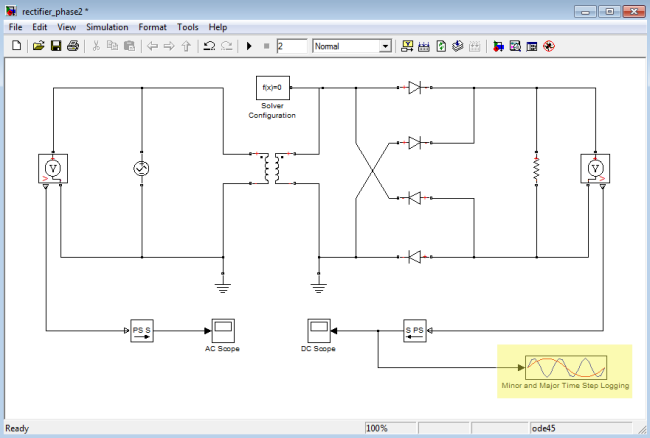
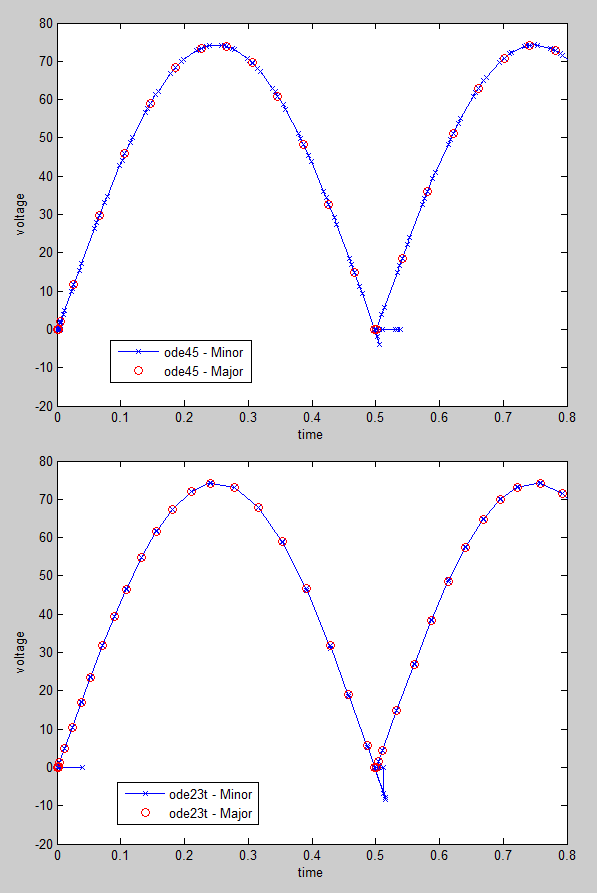
I employed this block on my tried-and-true rectifier model and ran a little experiment. I simulated with the ode45 and ode23t solvers and compared the results, which are shown below. As you can see, ode23t does a better job getting to the correct value on the first minor step (all the blue X marks are near the red circles). However, it takes roughly twice as many major time steps to get at the solution due to inherent differences in solver accuracies. Ultimately, which solver is better for my problem? I'll leave that as a topic of debate, but these results certainly help you understand the behavior and make an informed decision.
How does Guy's block produce figures such as these? He relies on a Level 2 MATLAB S-Function to store Simulink data to the MATLAB workspace. Check out LogMinorTimeStep.m to see how he leveraged the start, Output, and Terminate methods to accomplish his ends. It's a good example for learning about S-Functions if you've never done so.
Comments
Let us know what you think here or leave a comment for Guy.
What actually happens when you push that Play button within Simulink? How does Simulink go about solving your system? How do you troubleshoot when the algorithm is seemingly correct, and yet your results seem dubious?
I remember these thoughts percolating in my mind when I first began developing Simulink models. If you're curious about such things, a great place to start is to read the documentation on Simulating Dynamic Systems. Amongst a treasure trove of useful information, you'll discover that one of the key concepts of Simulink is major versus minor step. Once your simulation is complete, Simulink provides the results at specific points in time. These are results on the major time step. When using a Variable-step solver, results are accurate to the error tolerances you defined in Configuration Parameters.
What's not ordinarily presented to you are Simulink's intermediary calculations as it solves your system at each major step. For certain continuous time models, minor steps aid in convergence on a solution to the equations in your model. Anyone who's taken a numerical methods class will be familiar with this concept and has probably heard of Runge-Kutta solvers, one of many solver algorithms available within Simulink.
Nine times out of ten, you won't have to worry about what Simulink is calculating on a minor step. However, having this information can prove invaluable for debugging purposes, and it can aid in the age old question, "which solver should I choose for my problem?" There are various ways of getting access to minor step values, but I absolutely love the solution Guy has provided.
All you do is drag the Minor Time Step Logging block from the library into your model and connect it to the signal of interest. Run your simulation, and voila, you have a MATLAB figure displaying the major and minor step values. I tried it on numerous models with single and multidimensional signals...worked like a charm every time.

I employed this block on my tried-and-true rectifier model and ran a little experiment. I simulated with the ode45 and ode23t solvers and compared the results, which are shown below. As you can see, ode23t does a better job getting to the correct value on the first minor step (all the blue X marks are near the red circles). However, it takes roughly twice as many major time steps to get at the solution due to inherent differences in solver accuracies. Ultimately, which solver is better for my problem? I'll leave that as a topic of debate, but these results certainly help you understand the behavior and make an informed decision.

How does Guy's block produce figures such as these? He relies on a Level 2 MATLAB S-Function to store Simulink data to the MATLAB workspace. Check out LogMinorTimeStep.m to see how he leveraged the start, Output, and Terminate methods to accomplish his ends. It's a good example for learning about S-Functions if you've never done so.
Comments
Let us know what you think here or leave a comment for Guy.
- 범주:
- Picks









댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.