Get the Ship Stuck!
Contents
Get the Ship
We'll download the ship from a public source and isolate it.
ship = imread('https://e3.365dm.com/21/03/768x432/skynews-ever-given-suez-canal_5320248.jpg?20210327160438');
imshow(ship)

I could probably come up with a way to automatically segment the ship. But I only need to do it once, so I'll just draw the polygon and mask it.
if false % Draw polygon on border of ship p = drawpolygon; else load('p.mat', "p") imshow("eg.png") end

Mask the ship based on the polygon and apply that to the original image.
shipmask = poly2mask(p.Position(:, 1), p.Position(:, 2), height(ship), width(ship)); shipmask = imerode(shipmask, strel("disk", 2)); figure tiledlayout(2, 1, TileSpacing="compact", Padding="tight") nexttile imshow(shipmask) nexttile ship = ship.*cast(shipmask, class(ship)); imshow(ship)

Get the orientation from the ship mask and apply it to the original image.
shipprops = regionprops(shipmask, "Orientation")
shiphorizontal = imrotate(ship, -shipprops.Orientation);
figure
imshow(shiphorizontal)
shipprops =
struct with fields:
Orientation: 19.5882

Crop to just the ship
shipbbox = regionprops(logical(shiphorizontal(:, :, 1)), "BoundingBox")
shipthumb = imcrop(shiphorizontal, shipbbox.BoundingBox);
imshow(shipthumb)
shipbbox =
struct with fields:
BoundingBox: [181.5000 320.5000 427 67]

Download Lakeside Satellite Imagery
We'll download the satellite imagery from USGS for the region we care about. I'll interactively pick the regional limits for the area I care about.
if false % Interactively select limits w = webmap [latlim, lonlim] = wmlimits(w) else latlim = [42.2966508472710 42.3053796253471] lonlim = [-71.3800315706306 -71.3639383165411] end
latlim = 42.2967 42.3054 lonlim = -71.3800 -71.3639
Find the ortho layer and download it for this region.
ortho = wmsfind('usgsimageryonly', SearchField='serverurl'); [lakeside, lakesidereference] = wmsread(ortho, latlim=latlim, lonlim=lonlim); figure geoshow(lakeside, lakesidereference) axis tight

Prepare the Ship for "Docking"
I want to put the ship in the little lake between Rt 9 and the railroad track immediately adjacent to MathWorks' Lakeside campus. It looks like a ship orientation of about 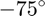 will work well.
will work well.
shipn75 = imrotate(shipthumb, -75,'nearest');
figure
imshow(shipn75);

We'll work in meters and need the dimensions of the ship. A quick web search says the length is 399.94m and the beam is 58.8m.
shiplength = 399.94; shipbeam = 58.8;
At the same time will check the ratio of length to width with that of our image.
props = regionprops(logical(shipn75(:,:,1)), "MajorAxisLength", "MinorAxisLength"); image_shipratio = props.MajorAxisLength/props.MinorAxisLength actual_shipratio = shiplength/shipbeam
image_shipratio =
6.7436
actual_shipratio =
6.8017
I'm happy with that(!) especially considering I just approximated the ship with a drawn polygon.
Now we need to figure out the size of this rotated image in meters. Assuming the ship was a perfect rectangle, we can calculate this size using some trigonometry. It's been awhile since I've done this so I broke out a trusty envelope and tried to remember soh-cah-toa. The equations for image dimensions are:
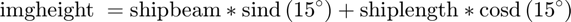
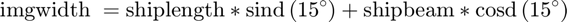
imgheightm = shipbeam*sind(15)+shiplength*cosd(15) imgwidthm = shiplength*sind(15)+shipbeam*cosd(15)
imgheightm = 401.5309 imgwidthm = 160.3085
Finally, we need to convert the background of the image to NaN so when we plot it shows as transparent. This is where all channels are 0.
shipoverlay = im2double(shipn75); shipoverlay(repmat(all(~shipoverlay, 3), [1 1 3])) = NaN;
Prepare Lakeside for a Ship
We need to project the satellite imagery from geographic coordinates (lat/lon) to cartesian coordinates (x/y in meters) to overlay the boat on it. We'll use the Mass State Plane coordinate reference system which is optimized for Massachusetts. A quick web search tells me that the code for this coordinate system is 26986.
p = projcrs(26986)
[latgrid, longrid] = geographicGrid(lakesidereference);
[xgrid, ygrid] = projfwd(p, latgrid, longrid);
figure
mapshow(xgrid,ygrid,lakeside)
axis tight
p =
projcrs with properties:
Name: "NAD83 / Massachusetts Mainland"
GeographicCRS: [1×1 geocrs]
ProjectionMethod: "Lambert Conic Conformal (2SP)"
LengthUnit: "meter"
ProjectionParameters: [1×1 map.crs.ProjectionParameters]
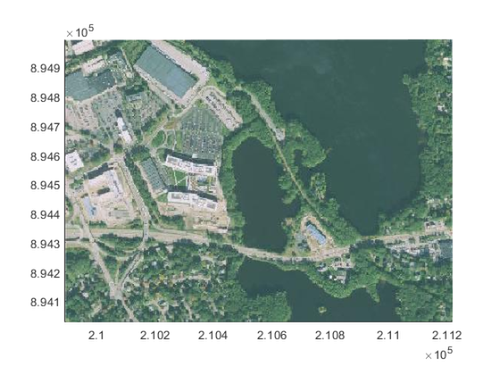
I'll use a datatip to find the upper left corner of where the boat should go. The live editor gives me the below code to reproduce this.
ax = gca; chart = ax.Children(1); datatip(chart, 210495, 894667);
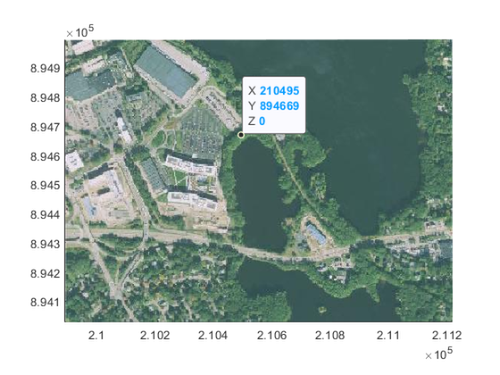
Since the map is now in projected coordinates, the x/y values represent meters. We can create map reference cells that describe the pixel size of the boat image and location which then makes plotting it easy.
xpt = 210495;
ypt = 894667;
mr = maprefcells([xpt xpt+imgwidthm], [ypt-imgheightm ypt], size(shipoverlay, [1 2]), ColumnsStartFrom="north")
mr =
MapCellsReference with properties:
XWorldLimits: [210495 210655.308527484]
YWorldLimits: [894265.469065182 894667]
RasterSize: [432 177]
RasterInterpretation: 'cells'
ColumnsStartFrom: 'north'
RowsStartFrom: 'west'
CellExtentInWorldX: 0.905697895390393
CellExtentInWorldY: 0.929469756523354
RasterExtentInWorldX: 160.3085274841
RasterExtentInWorldY: 401.530934818089
XIntrinsicLimits: [0.5 177.5]
YIntrinsicLimits: [0.5 432.5]
TransformationType: 'rectilinear'
CoordinateSystemType: 'planar'
ProjectedCRS: []
Stick the Ship!
And now we can finally plot the Lakeside image with the Ever Given overlaid on top to scale.
figure hold on mapshow(xgrid, ygrid, lakeside) s = mapshow(zeros(size(shipoverlay, [1 2])), mr, DisplayType="surface", CData=shipoverlay); axis tight xticks([]) yticks([])

- カテゴリ:
- Picks







コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。