Get the Ship Stuck!
Contents
Get the Ship
We'll download the ship from a public source and isolate it.
ship = imread('https://e3.365dm.com/21/03/768x432/skynews-ever-given-suez-canal_5320248.jpg?20210327160438');
imshow(ship)

I could probably come up with a way to automatically segment the ship. But I only need to do it once, so I'll just draw the polygon and mask it.
if false % Draw polygon on border of ship p = drawpolygon; else load('p.mat', "p") imshow("eg.png") end

Mask the ship based on the polygon and apply that to the original image.
shipmask = poly2mask(p.Position(:, 1), p.Position(:, 2), height(ship), width(ship)); shipmask = imerode(shipmask, strel("disk", 2)); figure tiledlayout(2, 1, TileSpacing="compact", Padding="tight") nexttile imshow(shipmask) nexttile ship = ship.*cast(shipmask, class(ship)); imshow(ship)

Get the orientation from the ship mask and apply it to the original image.
shipprops = regionprops(shipmask, "Orientation")
shiphorizontal = imrotate(ship, -shipprops.Orientation);
figure
imshow(shiphorizontal)
shipprops =
struct with fields:
Orientation: 19.5882

Crop to just the ship
shipbbox = regionprops(logical(shiphorizontal(:, :, 1)), "BoundingBox")
shipthumb = imcrop(shiphorizontal, shipbbox.BoundingBox);
imshow(shipthumb)
shipbbox =
struct with fields:
BoundingBox: [181.5000 320.5000 427 67]

Download Lakeside Satellite Imagery
We'll download the satellite imagery from USGS for the region we care about. I'll interactively pick the regional limits for the area I care about.
if false % Interactively select limits w = webmap [latlim, lonlim] = wmlimits(w) else latlim = [42.2966508472710 42.3053796253471] lonlim = [-71.3800315706306 -71.3639383165411] end
latlim = 42.2967 42.3054 lonlim = -71.3800 -71.3639
Find the ortho layer and download it for this region.
ortho = wmsfind('usgsimageryonly', SearchField='serverurl'); [lakeside, lakesidereference] = wmsread(ortho, latlim=latlim, lonlim=lonlim); figure geoshow(lakeside, lakesidereference) axis tight

Prepare the Ship for "Docking"
I want to put the ship in the little lake between Rt 9 and the railroad track immediately adjacent to MathWorks' Lakeside campus. It looks like a ship orientation of about 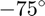 will work well.
will work well.
shipn75 = imrotate(shipthumb, -75,'nearest');
figure
imshow(shipn75);

We'll work in meters and need the dimensions of the ship. A quick web search says the length is 399.94m and the beam is 58.8m.
shiplength = 399.94; shipbeam = 58.8;
At the same time will check the ratio of length to width with that of our image.
props = regionprops(logical(shipn75(:,:,1)), "MajorAxisLength", "MinorAxisLength"); image_shipratio = props.MajorAxisLength/props.MinorAxisLength actual_shipratio = shiplength/shipbeam
image_shipratio =
6.7436
actual_shipratio =
6.8017
I'm happy with that(!) especially considering I just approximated the ship with a drawn polygon.
Now we need to figure out the size of this rotated image in meters. Assuming the ship was a perfect rectangle, we can calculate this size using some trigonometry. It's been awhile since I've done this so I broke out a trusty envelope and tried to remember soh-cah-toa. The equations for image dimensions are:
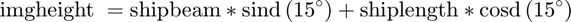
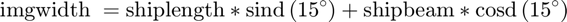
imgheightm = shipbeam*sind(15)+shiplength*cosd(15) imgwidthm = shiplength*sind(15)+shipbeam*cosd(15)
imgheightm = 401.5309 imgwidthm = 160.3085
Finally, we need to convert the background of the image to NaN so when we plot it shows as transparent. This is where all channels are 0.
shipoverlay = im2double(shipn75); shipoverlay(repmat(all(~shipoverlay, 3), [1 1 3])) = NaN;
Prepare Lakeside for a Ship
We need to project the satellite imagery from geographic coordinates (lat/lon) to cartesian coordinates (x/y in meters) to overlay the boat on it. We'll use the Mass State Plane coordinate reference system which is optimized for Massachusetts. A quick web search tells me that the code for this coordinate system is 26986.
p = projcrs(26986)
[latgrid, longrid] = geographicGrid(lakesidereference);
[xgrid, ygrid] = projfwd(p, latgrid, longrid);
figure
mapshow(xgrid,ygrid,lakeside)
axis tight
p =
projcrs with properties:
Name: "NAD83 / Massachusetts Mainland"
GeographicCRS: [1×1 geocrs]
ProjectionMethod: "Lambert Conic Conformal (2SP)"
LengthUnit: "meter"
ProjectionParameters: [1×1 map.crs.ProjectionParameters]
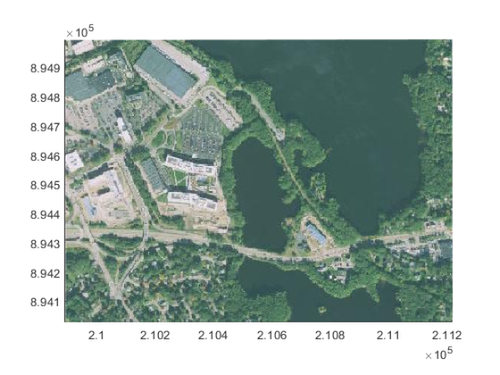
I'll use a datatip to find the upper left corner of where the boat should go. The live editor gives me the below code to reproduce this.
ax = gca; chart = ax.Children(1); datatip(chart, 210495, 894667);
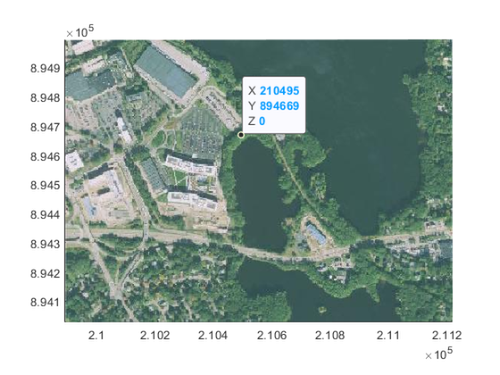
Since the map is now in projected coordinates, the x/y values represent meters. We can create map reference cells that describe the pixel size of the boat image and location which then makes plotting it easy.
xpt = 210495;
ypt = 894667;
mr = maprefcells([xpt xpt+imgwidthm], [ypt-imgheightm ypt], size(shipoverlay, [1 2]), ColumnsStartFrom="north")
mr =
MapCellsReference with properties:
XWorldLimits: [210495 210655.308527484]
YWorldLimits: [894265.469065182 894667]
RasterSize: [432 177]
RasterInterpretation: 'cells'
ColumnsStartFrom: 'north'
RowsStartFrom: 'west'
CellExtentInWorldX: 0.905697895390393
CellExtentInWorldY: 0.929469756523354
RasterExtentInWorldX: 160.3085274841
RasterExtentInWorldY: 401.530934818089
XIntrinsicLimits: [0.5 177.5]
YIntrinsicLimits: [0.5 432.5]
TransformationType: 'rectilinear'
CoordinateSystemType: 'planar'
ProjectedCRS: []
Stick the Ship!
And now we can finally plot the Lakeside image with the Ever Given overlaid on top to scale.
figure hold on mapshow(xgrid, ygrid, lakeside) s = mapshow(zeros(size(shipoverlay, [1 2])), mr, DisplayType="surface", CData=shipoverlay); axis tight xticks([]) yticks([])

- Category:
- Picks
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.