Multiresolution image pyramids and impyramid – part 1

Posted by Steve Eddins, April 2, 2019

9 views (last 30 days) | 0 Likes | 4 comments

There's a function in the Image Processing Toolbox that I'm not especially fond of: impyramid.

I shouldn't tell you who designed this function, but I'll give you a hint: his initials are "Steve Eddins."

Years ago, we had occasional user requests for creating multiresolution image pyramids, such as Gaussian pyramids and Laplacian pyramids. I thought these requests would be easy to satisfy by impyramid, but I was wrong. I was reminded of the problems by some code written by one our Pilot engineers, Steve Kuznicki. Steve made a nice of use impyramid to implement a multiresolution image blending method, but weaknesses in the design of impyramid made some of the code awkward. Today I want to discuss those weaknesses. In a follow-up post later, I'll demonstrate some possible improvements.

I'll start by explaining multiresolution pyramids. Below an example of one. This form is sometimes called a lowpass pyramid.

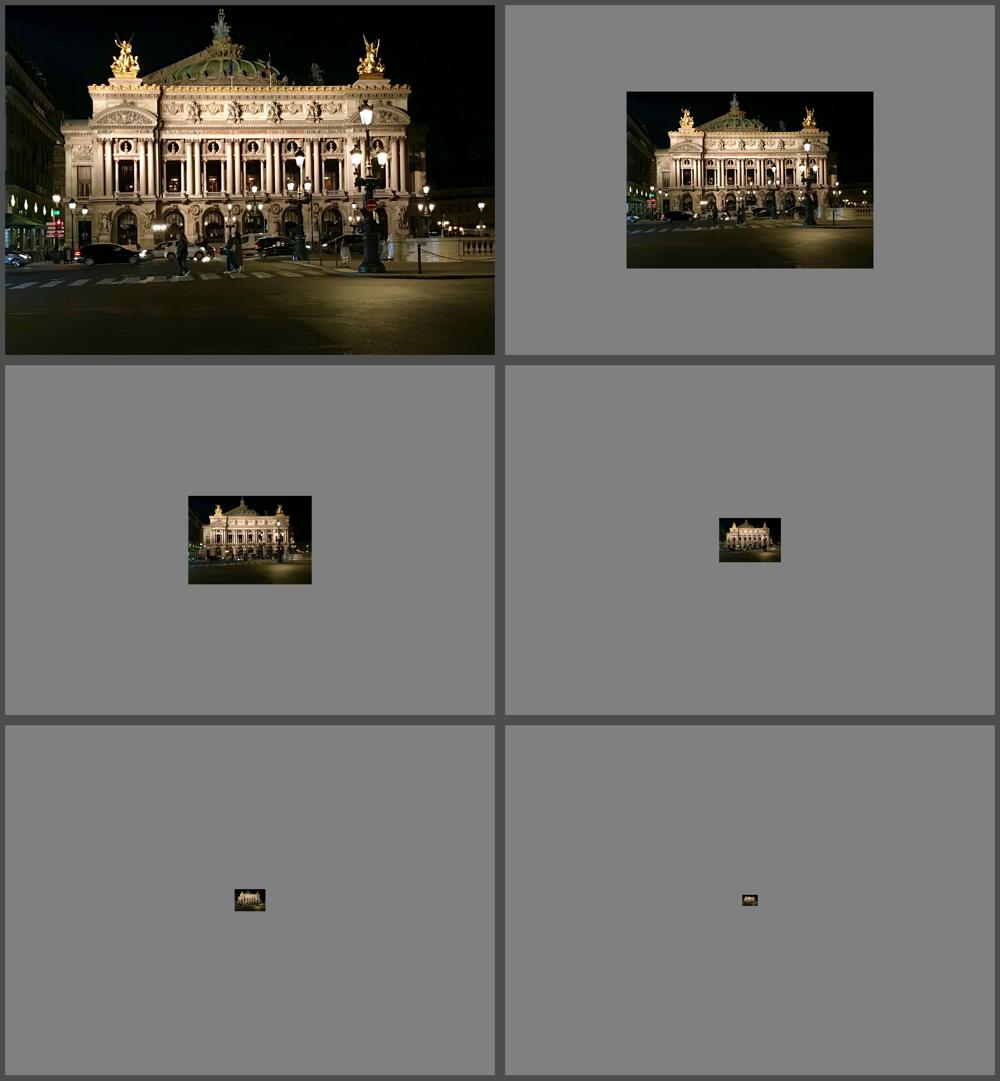
The original image is shown in the upper left. The image is lowpass filtered and then subsampled by a factor of 2 in each direction to form the image in the upper right. That process is repeated several times, reaching the tiny version of the original image at the lower right.

So, I think "multiresolution pyramid" and "lowpass pyramid" are both sensible terms, but why is this frequently called a "Gaussian pyramid"? The answer comes from an implementation technique described in Burt, "Fast Filter Transforms for Image Processing," Computer Graphics and Image Processing, vol. 16, pp. 20-51, 1981. Burt described a procedure for forming a multiresolution pyramid by filtering at each step with the kernel $h_1(x)$ in Fig. 2 from the paper:

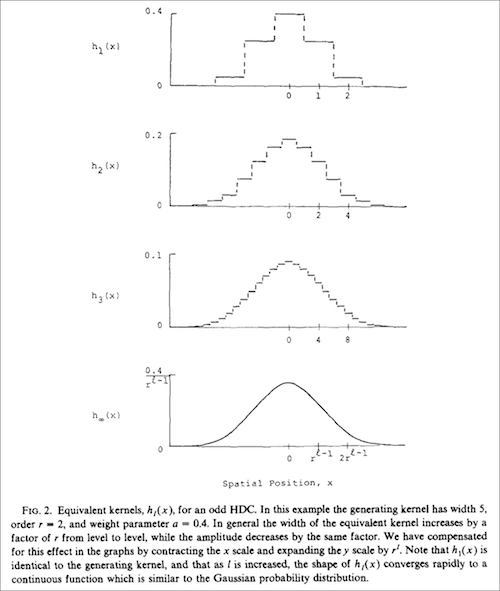
The coefficients of $h_1(x)$ are $1/4 - a/2$, 0.25, and $a$, with typical values for $a$ around 0.4.

As you successively apply this filter at each stage of a multiresolution pyramid, the overall effect becomes similar to filtering with a continuous Gaussian-shaped kernel, and this is where the name Gaussian pyramid comes from.

At the time this paper was written, computers were vastly slower than they are now, especially with floating-point computation. The floating-point convolution of a 512x512 image (considered large then, and considered quite small now) with a filter of modest size could take minutes.

That explains part of the significance of Burt's implementation method. Not only is the filter applied at each pyramid stage very small, but when $a = 0.375$, all the filter coefficients are exact binary fractions and so can be implemented by direct processor bit-shift instructions on the integer pixel values. That allowed for reasonably fast implementations on the computers of that time.

When I try to put impyramid to good use, or when I have seen other people try to use it, the following problems stand out to me:

Each call to the function impyramid implements a single level, either a reduction or an expansion. That leaves it up to the caller to handle a lot tedious code for deciding how many levels there should be, keeping track of the size of the original image, and handling cases where the original image dimensions are not powers-of-two multiples of the size of the smallest image in the pyramid.
When you call impyramid to reduce an image by a level, and then you call impyramid on the reduced image to expand it, you don't get the same image size that you started with. For example, if you start with a 1360x1904 image, you end up with a 1359x1903 image after reducing and then expanding again. I distinctly remember convincing myself that there was a legit reason for this. Sigh. It just adds a lot more tedious image padding code around many uses of impyramid.
As image resizing filters go, the one used by impyramid (described above) is not a very good one for downsampling applications. I understand its use in 1981, but on modern computers, we can do better.
Finally, there needs to be an easier way to visualize the multiresolution pyramid. This would be useful as an aid to general understanding, as well as to debugging specific issues. The imtile function that I discussed on March 17 doesn't quite do it because it automatically resizes each image tile to be the same size.

Extra credit: Do you know what building is in the image above? If so, leave a note in the comments.

Published with MATLAB® R2019a