The functions meshgrid and repmat have a long and rich history in MATLAB. Today, I'll try to convince you to use them less.
meshgrid
The function meshgrid is typically used to take a vector of x-coordinates and a vector of y-coordinates and turn them into two matrices, X and Y, that can be used to compute a function of two variables. Here is a small example.
[X,Y] = meshgrid(x,y)
0 0 0
10 10 10
20 20 20
30 30 30
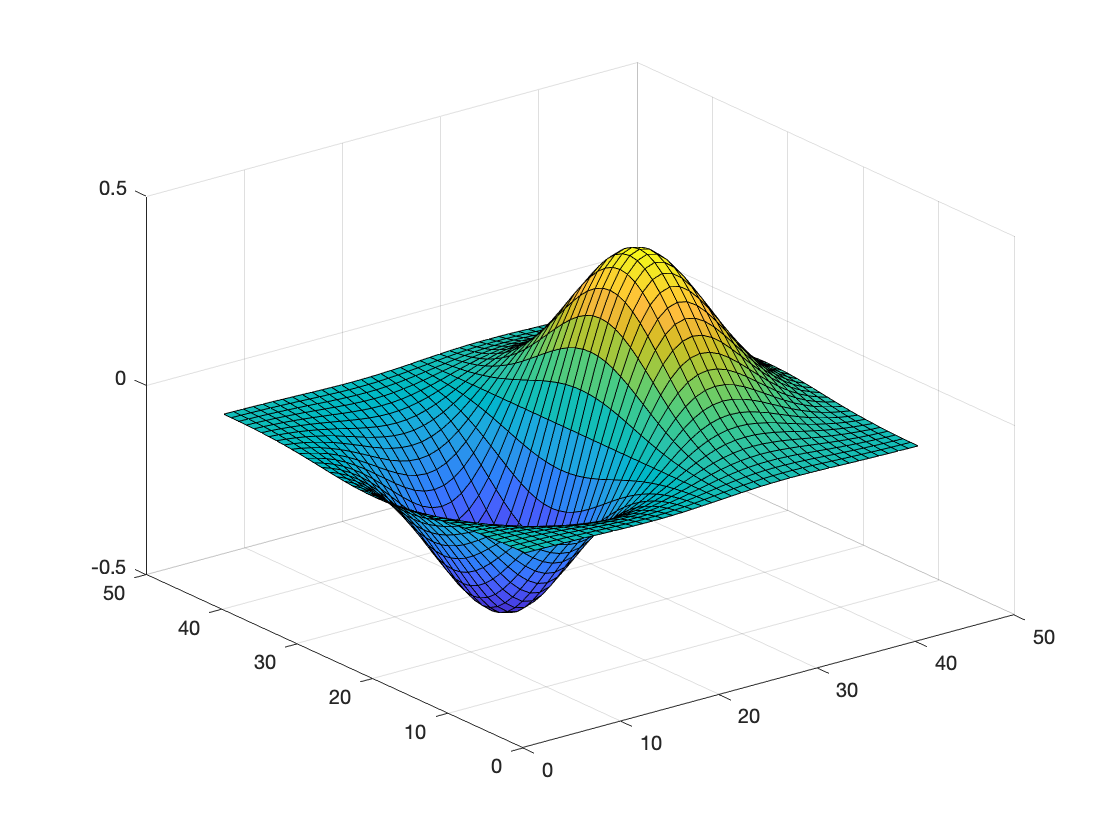
Here is another example that illustrates how meshgrid is typically used. The example, taken from the 2nd edition (2009) of Digital Image Processing Using MATLAB, constructs a surface plot of the function $ f(x,y) = xe^{-(x^2 + y^2)} $.
Z = X.*exp(-(X.^2 + Y.^2));
The variables x and y are vectors, and the variables X and Y are matrices:
whos x y X Y
Name Size Bytes Class Attributes
X 41x41 13448 double
Y 41x41 13448 double
x 1x41 328 double
y 1x41 328 double
The function meshgrid has been used to construct same-sized matrices so that they can be combined together in various element-wise arithmetic operations on matrices that represent two spatial coordinates.
repmat
The function name repmat is an abbrevation of "replicate matrix." One common use for repmat is to replicate a vector to be the size of a matrix, or to replicate a matrix to be the size of a 3-D array. A classic example is to subtract the column means from a matrix:
A = rand(4)
0.8147 0.6324 0.9575 0.9572
0.9058 0.0975 0.9649 0.4854
0.1270 0.2785 0.1576 0.8003
0.9134 0.5469 0.9706 0.1419
col_means = mean(A,1)
0.6902 0.3888 0.7627 0.5962
B = repmat(col_means,size(A,1),1)
0.6902 0.3888 0.7627 0.5962
0.6902 0.3888 0.7627 0.5962
0.6902 0.3888 0.7627 0.5962
0.6902 0.3888 0.7627 0.5962
C = A - B
0.1245 0.2435 0.1949 0.3610
0.2156 -0.2913 0.2022 -0.1108
-0.5632 -0.1103 -0.6050 0.2041
0.2232 0.1581 0.2079 -0.4543
Five-Year Anniversary of MATLAB Arithmetic Operator Change
Five years ago, with the R2016b release of MATLAB, some MATLAB operators and functions were generalized in a way that made many uses of meshgrid and repmat no longer necessary. With that release, operators such as + and - that take two operands could automatically handle operands with different sizes, as long as the size differences took a specific form. In the example above, A has size 4x4, and col_means has size 1x4. Prior to the R2016b release, the expression A - col_means would produce an error because of the mismatched sizes. Starting in R2016b, though, arithmetic operators (and some other operators and functions) can automatically match up different sizes when one or the other operand has a dimension of 1 in the mismatched dimension.
This means that you no longer need to call repmat to subtract the column means from a matrix. You can do it just with the - operator:
C = A - mean(A,1)
0.1245 0.2435 0.1949 0.3610
0.2156 -0.2913 0.2022 -0.1108
-0.5632 -0.1103 -0.6050 0.2041
0.2232 0.1581 0.2079 -0.4543
Also, you usually no longer need to use meshgrid as shown above to compute a function of two variables. The code in the previous example can now be written as:
Z = x.*exp(-(x.^2 + y.^2));
The 3rd edition (2020) of Digital Image Processing Using MATLAB was revised accordingly.
For More Information
For more information about the details and history of this change, I recommend these sources. The first three of these appear on Loren Shure's Art of MATLAB blog; the first two were guest-written by me. The last source is a MATLAB documentation page.
Two More Examples
In 2011, I wrote some blog posts about generating a test image that some call a zone plate. I also put the related code on the File Exchange as the function imzoneplate. Here is the key math portion of the original implementation: The hypot function, though, supports implicit expansion now, and so the call to meshgrid is not necessary. The first couple of lines can be rewritten as:
The 2nd edition of Digital Image Processing Using MATLAB included a code fragment intended to compute the Euclidean distance between every row of a pxn matrix X and a 1xn vector y:
This can now be written without the call to repmat:
So, the next time you find yourself reaching for meshgrid or repmat -- maybe you don't need it!








댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.