MATLAB arithmetic expands in R2016b
With pleasure, I introduce today's guest blogger, my colleague, Steve Eddins. He has been heavily involved in image processing capabilities in our tools and more recently has also contributed substantially to designing additions and improvements to the MATLAB language.
Earlier this summer, I was writing some color-space conversion code. At one point in the code, I had a Px3 matrix called RGB, which contained P colors, one per row. I also had a 1x3 vector, v. I needed to multiply each column of RGB by the corresponding element of v, like this:
RGB_c = [RGB(:,1)*v(1) RGB(:,2)*v(2) RGB(:,3)*v(3)];
But since I was using an internal developer build of MATLAB R2016 (released on September 14), I didn't type the code above. Instead, I typed this:
RGB_c = RGB .* v;
In R2016a and older MATLAB releases, that line of code produced an error:
>> RGB_c = RGB .* v Error using .* Matrix dimensions must agree.
In the new release, though, MATLAB implicitly expands the vector v to be the same size as the matrix RGB and then carries out the elementwise multiplication. I say "implicitly" because MATLAB does not actually make an in-memory copy of the expanded vector.
Today I want to explain this new implicit expansion behavior of MATLAB arithmetic operators (and some functions). I will talk about how it works and why we did it. For the next part of the discussion, I'll use an example that almost everyone at MathWorks uses when talking about this topic: subtracting the column means from a matrix.
Contents
Subtracting Column Means: Decade by Decade
Suppose you have a matrix A.
A = rand(3,3)
A =
0.48976 0.70936 0.6797
0.44559 0.75469 0.6551
0.64631 0.27603 0.16261
And suppose you want to modify each column of A by subtracting the column's mean. The mean function conveniently gives you each of the column means:
ma = mean(A)
ma =
0.52722 0.58003 0.49914
But since ma is not the same size as A and is not a scalar, you couldn't just subtract ma from A directly. Instead, you had to expand ma to be the same size as A and then do the subtraction.
In the first decade of MATLAB, expert users typically used an indexing technique called Tony's Trick to do the expansion.
ma_expanded = ma(ones(3,1),:)
ma_expanded =
0.52722 0.58003 0.49914
0.52722 0.58003 0.49914
0.52722 0.58003 0.49914
A - ma_expanded
ans =
-0.037457 0.12934 0.18057
-0.081635 0.17466 0.15596
0.11909 -0.304 -0.33653
In the second decade (roughly speaking) of MATLAB, most people started using a function called repmat (short for "replicate matrix") to do the expansion.
ma_expansion = repmat(ma,3,1)
ma_expansion =
0.52722 0.58003 0.49914
0.52722 0.58003 0.49914
0.52722 0.58003 0.49914
Using the function repmat was more readable than using Tony's Trick, but it still created the expanded matrix in memory. For really large problems, the extra memory allocation and memory copy could noticeably slow down the computation, or even result in out-of-memory errors.
So, in the third decade of MATLAB, we introduced a new function called bsxfun that could do the subtraction operation directly without making an expanded vector in memory. You call it like this:
bsxfun(@minus,A,ma)
ans =
-0.037457 0.12934 0.18057
-0.081635 0.17466 0.15596
0.11909 -0.304 -0.33653
The "bsx" in the function name refers "Binary Singleton Expansion," where the term "Binary" in this context refers to operators that take two inputs. (No, it's not anyone's favorite function name.)
This function works and has been used quite a bit. As of a year ago, there were about 1,800 uses of bsxfun in 740 files.
But there were complaints about bsxfun.
bsxfun Pains
Besides the awkward name, there were other usability and performance issues associated with bsxfun.
- Not many people know about this function. It's not at all obvious that one should go looking for it when looking for help with subtraction.
- Using bsxfun requires a level of programming abstraction (calling one function to apply another function to a set of inputs) that seems mismatched with the application (basic arithmetic).
- Using bsxfun requires relatively advanced knowledge of MATLAB programming. You have to understand function handles, and you have to know about the functional equivalents of MATLAB arithmetic operators (such as plus, minus, times, and rdivide).
- It is more difficult for the MATLAB Execution Engine builders to generate code that is as efficient as the code for basic arithmetic.
- Code that uses bsxfun doesn't appear mathematical. (Some go so far as to call it ugly.)
And so, fourteen years after Cleve Moler originally proposed doing it, we have changed MATLAB two-input arithmetic operators, logical operators, relational operators, and several two-input functions to do bsxfun-style implicit expansion automatically whenever the inputs have compatible sizes.
Compatible Sizes
The expression A - B works as long as A and B have compatible sizes. Two arrays have compatible sizes if, for every dimension, the dimension sizes of the inputs are either the same or one of them is 1. In the simplest cases, two array sizes are compatible if they are exactly the same or if one is a scalar.
Here are some illustrations of compatible sizes for different cases.
- Two inputs which are exactly the same size.

- One input is a scalar.

- One input is a matrix, and the other is a column vector with the same number of rows.
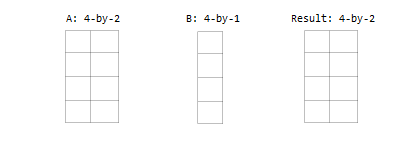
- One input is a column vector, and the other is a row vector. Note that both inputs are implicitly expanded in this case, each in a different direction.

- One input is a matrix, and the other is a 3-D array with the same number of rows and columns. Note that the size of the matrix A in the third dimension is implicitly considered to be 1, and so A can be expanded in the third dimension to be the same size as B.

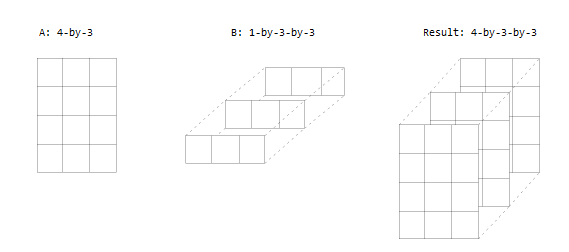
- One input is a matrix, and the other is a 3-D array. The dimensions are all either the same or one of them is 1. Note that this is another case where both inputs are implicitly expanded.
Supported Operators and Functions
Here is the initial set of MATLAB operators and functions that now have implicit expansion behavior.
+ - .* ./ .\ .^ < <= > >= == ~= | & xor bitor bitand bitxor min max mod rem hypot atan2
I anticipate that other functions will be added to this set over time.
Objections
This change to MATLAB arithmetic was not without controversy at MathWorks. Some people were concerned that users might have written code that somehow depended on these operators producing an error in some cases. But after examining our own code base, and after previewing the change in both the R2016a and R2016b Prereleases, we did not see significant compatibility issues arise in practice.
Other people thought that the new operator behavior was not sufficiently based on linear algebra notation. However, instead of thinking of MATLAB as a purely linear algebra notation, it is more accurate to think of MATLAB as being a matrix and array computation notation. And in that sense, MATLAB has a long history of inventing notation that became widely accepted, including backslash, colon, and various forms of subscripting.
Finally, some were concerned about what would happen when users tried to add two vectors without realizing that one is a column and the other is a row. In earlier versions of MATLAB, that would produce an error. In R2016b, it produces a matrix. (I like to call this matrix the outer sum of the two vectors.) But we believed that this problem would be immediately noticed and easily corrected. In fact, I think it's easier to notice this problem than when you mistakenly use the * operator instead of the .* operator. Also, the relatively new protective limit on array sizes in MATLAB (Preferences -> MATLAB -> Workspace -> MATLAB array size limit) prevents MATLAB from trying to form an extremely large matrix that might cause an out-of-memory condition.
Implicit Expansion in Practice
As part of the research we did before deciding to make this change, we reviewed how people use bsxfun. I'll finish the post by showing you what some of the most common uses of bsxfun look like when you rewrite them using implicit expansion in R2016b.
Apply a mask to a truecolor image.
% mask: 480x640 % rgb: 480x640x3
% OLD rgb2 = bsxfun(@times,rgb,mask);
% NEW rgb2 = rgb .* mask;
Normalize matrix columns (subtract mean and divide by deviation).
% X: 1000x4 mu = mean(X); sigma = std(X);
% OLD Y = bsxfun(@rdivide,bsxfun(@minus,X,mu),sigma);
% NEW Y = (X - mu) ./ sigma;
Compute the pairwise distance matrix.
For two sets of vectors, compute the Euclidean distance between every vector pair.
% X: 4x2 (4 vectors) % Y: 3x2 (3 vectors) X = reshape(X,[4 1 2]); Y = reshape(Y,[1 3 2]);
% OLD m = bsxfun(@minus,X,Y); D = hypot(m(:,:,1),m(:,:,2));
% NEW m = X - Y; D = hypot(m(:,:,1),m(:,:,2));
Compute outer sum.
This example is from the implementation of the toeplitz function. See also my 25-Feb-2008 post on neighbor indexing for another application.
cidx = (0:m-1)'; ridx = p:-1:1;
% OLD ij = bsxfun(@plus,cidx,ridx);
% NEW ij = cidx + ridx;
Find integers that are multiples of each other.
This example is from the computation of the Redheffer matrix in the gallery function. It illustrates implicit expansion behavior in a function as opposed to an operator.
i = 1:n;
% OLD A = bsxfun(@rem,i,i') == 0;
% NEW A = rem(i,i') == 0;
You Asked for It
I want to finish with a shout out to all the MATLAB users who have asked for this behavior over the years. File Exchange contributor Yuval spoke for all of you when he included this comment inside the implementation of his submission:
% We need full singleton expansion everywhere. Why isn't % it the case that % % [1 2] + [0 1]' == [1 2;2 3] ? % % bsxfun() is a total hack, and polluting % everybody's code.
Yuval, this one's for you.
Readers, have you used bsxfun before? Will you make use of the new arithmetic behavior? Let us know here.
- Category:
- New Feature,
- Vectorization
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.