Jähne test pattern – take 3
Earlier today I told you that I was feeling a little dense because I couldn't figure out the right parameters to use in the tanh term of this test pattern:

(This is equation 10.63 in Practical Handbook on Image Processing for Scientific Applications by Bernd Jahne.)
I'm grateful to reader Alex H for quickly enlightening me. He described  as an approximation to a step function, where a is the location of the step and w is the width of the transition. That was very helpful.
as an approximation to a step function, where a is the location of the step and w is the width of the transition. That was very helpful.
I've also realized that I misinterpreted the meaning of 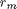 . In the book this is described as the "maximum radius of the pattern," and I assumed this would be fixed as the distance
from the center of the square image to one of its corners. But now I realize that the author intended for this to be an adjustable
parameter. That is, one can set
. In the book this is described as the "maximum radius of the pattern," and I assumed this would be fixed as the distance
from the center of the square image to one of its corners. But now I realize that the author intended for this to be an adjustable
parameter. That is, one can set 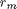 so that the maximum instantaneous frequency is reached closer to the center than at the image corners.
so that the maximum instantaneous frequency is reached closer to the center than at the image corners.
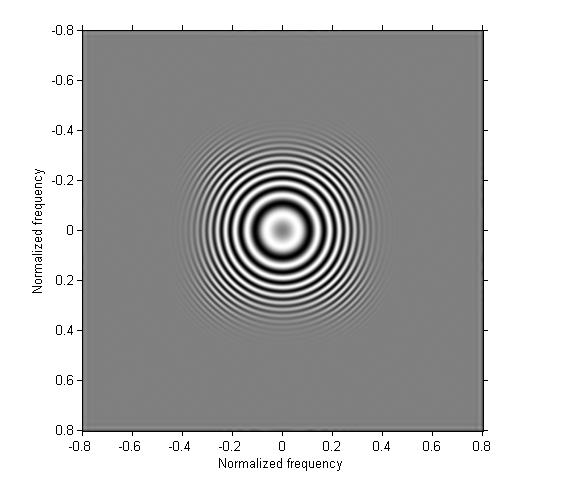
For example, I can set the parameters so that the maximum instantaneous frequency of  is reached in the center of the image edges, and then the tapering function prevents aliasing artifacts from appearing as
you move out to the corners. The book's figure 10.23 is based on maximum instantaneous frequency of
is reached in the center of the image edges, and then the tapering function prevents aliasing artifacts from appearing as
you move out to the corners. The book's figure 10.23 is based on maximum instantaneous frequency of  (a period of 2.5 samples) reached at the edges, so I'll use that.
(a period of 2.5 samples) reached at the edges, so I'll use that.
[x,y] = meshgrid(-200:200); km = 0.8*pi; rm = 200; w = rm/10; term1 = sin( (km * r.^2) / (2 * rm) ); term2 = 0.5*tanh((rm - r)/w) + 0.5; g = term1 .* term2; imshow(g,[])

Finally, a result that looks like the figure in the book!
Thanks again, Alex.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.