Spatial transformations: Terminology and notation
"Terminology and notation" - is there a more boring way to start a topic? Unfortunately it's necessary, because there is a lot of variation in terms and equations from book to book and paper to paper. Some of the "frequently-asked questions" arise from simple confusion over notations and conventions. Even the topic itself is a source of confusion. Start with either the word geometric or spatial, and then add one of these words: transform, transformation, or warp. The Image Processing Toolbox Users Guide uses spatial transformation, while Digital Image Processing Using MATLAB uses geometric transformation. I'll try to stick with spatial transformation.
This picture shows several of the most important conceptual elements:

[Edited 31-Jan-2006 to fix typo in diagram]
There are two Cartesian coordinate systems, input space and output space. I'll consistently use (u,v) for input space and (x,y) for output space.
A forward transformation, shown as T{ }, maps a location in input space to a location in output space: (x0, y0) = T{ (u0, v0) }.
A inverse transformation, shown as T-1{ }, maps a location in output space to a location in input space: (u1, v1) = T-1{ (x1, y1) }.
It's important to refer to a diagram like this. It can help you remember:
- Is an (x,y) location in input space or output space?
- Is the u axis horizontal or vertical?
- Does the vertical axis point up or down?
If you compare what the Image Processing Toolbox does, or what I write here, with another reference, be sure to determine exactly what the notational conventions are in the other reference. Figure out how they differ with the toolbox conventions. That'll help you figure out why your output image is upside down, or why it was stretched in the horizontal direction when you expected it to be stretched in the vertical direction.
Please note that Digital Image Processing Using MATLAB uses (w, z) instead of (u, v) for input-space coordinates. That's because (u, v) is used elsewhere in the book as frequency-domain coordinates.
- Category:
- Spatial transforms
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building



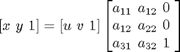




Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.