Graph Object of 48 USA States
Create a MATLAB® graph object from information about neighbors among the 48 contiguous states in the USA.
Contents
Car Talk Puzzler
A few years ago, MathWorks asked Tom and Ray Magliozzi, MIT alumni and hosts of the popular show Car Talk on National Public Radio, to come to our offices and meet some visiting students. They said yes on one condition. They figured MathWorkers would be a good source of new material for the puzzler segment of their show. It turned out that we had only one puzzle to offer that they hadn't heard before. But one was enough, and they came for the visit.
Here is that puzzle.
My friend tells me that she is about to take a road trip. She plans to visit each of the 48 contiguous states in the USA exactly once. She tells me she is going to start someplace in the West and doesn't tell me where she is going to finish. However, I am able to agree to meet her in the last state she will visit. Which state is that?
I will reveal the state later in this post, but try to answer the puzzle before I do. (Readers who are not familiar with USA geography don't have to worry -- few Americans can provide the answer.)
States
The web site of John Burkardt at Florida State University is a tremendous repository of software, data sets and other goodies. I am going to use state neighbors. The first column in this file provides the two-letter abbreviations of the names of the 48 contiguous states.
S = get_state_neighbors;
names = S{:,1};
fmt = [repmat('%s ',1,16) '\n'];
fprintf(fmt,names)
AL AZ AR CA CO CT DE FL GA ID IL IN IA KS KY LA ME MD MA MI MN MS MO MT NE NV NH NJ NM NY NC ND OH OK OR PA RI SC SD TN TX UT VT VA WA WV WI WY
The list is ordered alphabetically by the full state name, so Wyoming is last.
last = names(end)
last =
"WY"
Neighboring States
Burkardt's data also gives us the neighbors of each state. We can form an adjacency matrix A where A(i,j) is one if states i and j share a common border and zero otherwise.
A = adjacency(S);
For example, Wyoming has six neighbors.
last_neighbors = names(A(end,:))
last_neighbors =
6×1 string array
"CO"
"ID"
"MT"
"NE"
"SD"
"UT"
Every good adjacency deserves a spy plot.
spy(A)
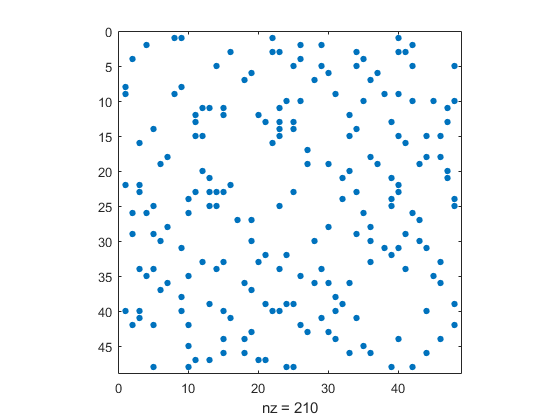
The last row (and column) has six nonzeros for Wyoming's six neighbors.
Most Neighbors
Which states have the most neighbors?
num_neigh = sum(A);
max_num_neigh = max(num_neigh)
max_neigh = names(num_neigh == max_num_neigh)
max_num_neigh =
8
max_neigh =
2×1 string array
"MO"
"TN"
Missouri and Tennessee each have eight neighbors.
Fewest Neighbors
Which state has the fewest neighbors?
min_num_neigh = min(num_neigh)
min_neigh = names(num_neigh == min_num_neigh)
min_num_neigh =
1
min_neigh =
"ME"
Maine has only one neighbor, namely New Hampshire. This provides the answer to the MathWorks Car Talk puzzle. My friend's trip must either start or finish in in Maine. Once she's in Maine, she can't leave without going through New Hampshire. Since she is starting in the West, she must finish in Maine.
Graph
Every adjacency matrix also has an associated graph.
G = graph(A,cellstr(names))
G =
graph with properties:
Edges: [105×1 table]
Nodes: [48×1 table]
The default layout for plotting this graph is force, which uses attractive and repulsive forces on the nodes.
plot(G)
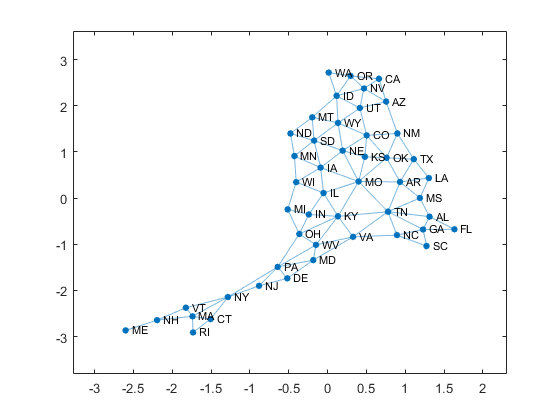
Interchange the axes by switching the viewpoint.
view(-90,-90)
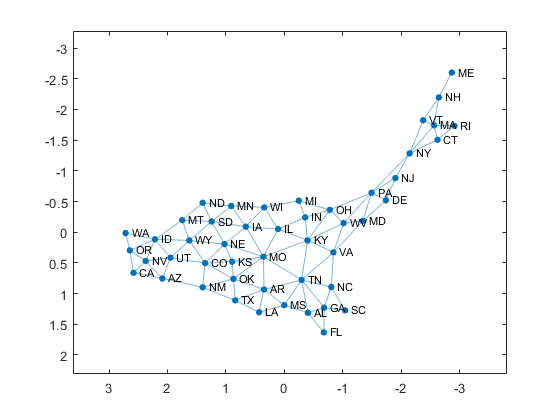
The plot now resembles the United States. California, Oregon and Washington are on the west coast. Florida is a peninsula in the southeast. The New England states dominate the northeast. MO and TN show off their many neighbors.
Utah, Arizona, New Mexico and Colorado are the corners of one of two quadrilaterals in the graph, mimicking their actual meeting at Four Corners. The other quadrilateral involves the four states that surround Lake Michigan.
All this without any coordinates, just knowing the connectivity of neighboring states.
Next
My next post will add the coordinates of the state capitals and tackle the classic Traveling Salesman Problem.
Thanks
Thanks to John Burkhardt for his data sets and for pointing out that the wording of the puzzle needs to preclude starting in Maine.








コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。