R-squared. Is Bigger Better?
The coefficient of determination, R-squared or R^2, is a popular statistic that describes how well a regression model fits data. It measures the proportion of variation in data that is predicted by a model. However, that is all that R^2 measures. It is not appropriate for any other use. For example, it does not support extrapolation beyond the domain of the data. It does not suggest that one model is preferable to another.
I recently watched high school students participate in the final round of a national mathematical modeling competition. The teams' presentations were excellent; they were well-prepared, mathematically sophisticated, and informative. Unfortunately, many of the presentations abused R^2. It was used to compare different fits, to justify extrapolation, and to recommend public policy.
This was not the first time that I have seen abuses of R^2. As educators and authors of mathematical software, we must do more to expose its limitations. There are dozens of pages and videos on the web describing R^2, but few of them warn about possible misuse.
R^2 is easily computed. If y is a vector of observations, f is a fit to the data and ybar = mean(y), then
R^2 = 1 - norm(y-f)^2/norm(y-ybar)^2
If the data are centered, then ybar = 0 and R^2 is between zero and one.
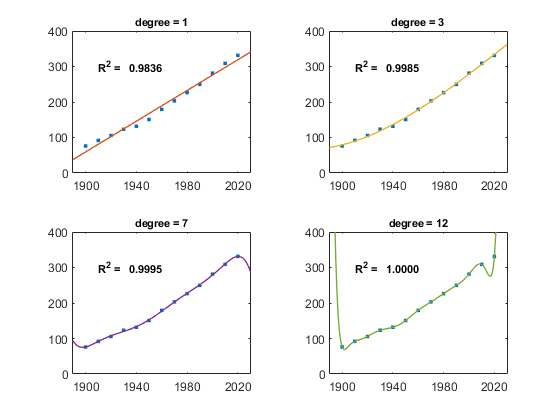
One of my favorite examples is the United States Census. Here is the population, in millions, every ten years since 1900.
t p ____ _______ 1900 75.995 1910 91.972 1920 105.711 1930 123.203 1940 131.669 1950 150.697 1960 179.323 1970 203.212 1980 226.505 1990 249.633 2000 281.422 2010 308.746 2020 331.449
There are 13 observations. So, we can do a least-squares fit by a polynomial of any degree less than 12 and can interpolate by a polynomial of degree 12. Here are four such fits and the corresponding R^2 values. As the degree increases, so does R^2. Interpolation fits the data exactly and earns a perfect core.
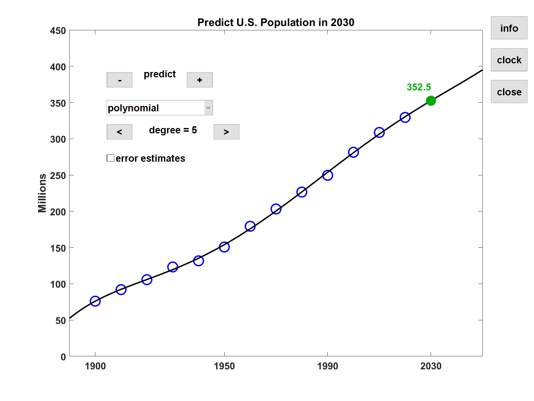
Which fit would you choose to predict the population in 2030, or even to estimate the population between census years?
R2_census
Thanks to Peter Perkins and Tom Lane for help with this post.








댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.