When the starting point of Newton's method is not close to a zero of the function, the global behavior can appear to be unpredictable. Contour plots of iteration counts to convergence from a region of starting points in the complex plane generate thought-provoking fractal images. Our examples employ the subject of two recent posts, the historic cubic $x^3-2x-5$. ... read more >>

Use the historic cubic polynomial $x^3 - 2x - 5$ to test a few zero-finding algorithms. ... read more >>

MATLAB adds capability to search for an interval with a sign change.... read more >>

Richard Brent's improvements to Dekker's zeroin algorithm, published in 1971, made it faster, safer in floating point arithmetic, and guaranteed not to fail. ... read more >>

Th. J. Dekker's zeroin algorithm from 1969 is one of my favorite algorithms. An elegant technique combining bisection and the secant method for finding a zero of a function of a real variable, it has become fzero in MATLAB today. This is the first of a three part series.... read more >>

Augustin (Austin) Dubrulle deserves to be better known in the numerical linear algebra community. His version of the implicit QR algorithm for computing the eigenvalues of a symmetric tridiagonal matrix that was published in a half-page paper in Numerische Mathematik in 1970 is faster than Wilkinson's version published earlier. It is still a core algorithm in MATLAB today. ... read more >>

This is the third in a multi-part series on the MATLAB random number generators. MATLAB has used variants of George Marsaglia's ziggurat algorithm to generate normally distributed random numbers for almost twenty years. ... read more >>

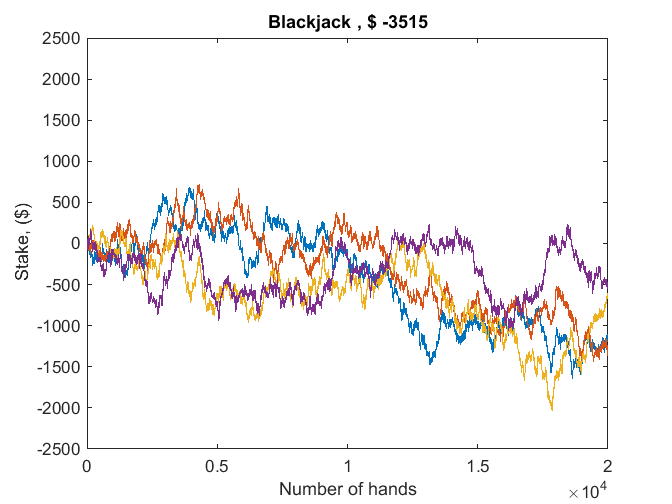
This is the second of a multi-part series about the MATLAB random number generators. If you ask for help rng, you will get lots of information, including the fact that there are three modern generators.... read more >>

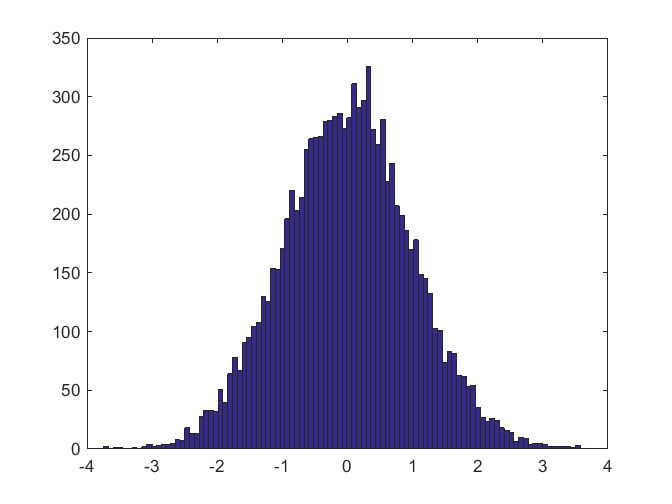
This is the first of a multi-part series about the MATLAB random number generators.... read more >>

Single and double precision are combined to facilitate a triple precision accumulated inner product.... read more >>