Robot Game-Playing in MATLAB
A story about just-in-time expertise. Sometimes the best learning is no learning.
COMPUTERS, CHESS, AND GO
I read an article in IEEE Spectrum about computer programs that play Go (AIs Have Mastered Chess. Will Go Be Next?). If you review the history of game-playing computers, you’ll see that chess programs improved steadily until eventually they could beat the best human players. Go programs, on the other hand, have been stuck at a level of play that was nowhere close to the best human. Why is that?
The basic element of a game-playing program is the look-ahead. Essentially, the program says “If I move here, is that better or worse than if I move there?” In chess, this is straightforward to evaluate. But in Go, this basic look-ahead strategy doesn’t work so well. It’s much harder to evaluate whether one board position is stronger than another.
But recently, Go programs have started to get much better. What happened?
TWO IDIOTS FINISH THE GAME
Go programs have improved by applying a Monte Carlo technique. It’s nothing like how a human plays, but it works remarkably well. And it only works because we can ask the computer to do a lot of dumb stuff very quickly. I call it “Two Idiots Finish the Game”.
Consider the following situation. You’ve reached a critical point in the game. We’ll call it position X. You’re considering
move A and move B. Which one should you make? Now instead of looking just one move ahead, play the game all the way to completion. But there’s an obvious problem with this. If you’re not smart enough to figure out your next move, how can you play an entire game? Simple: just ask two idiots to make random (but legal) moves until one of them wins. Then return the game to position X and have them play again. And again. And again and again. Sometimes they start with move A, and sometimes B. After your speedy but not-so-clever friends have played a few thousand games, examine the record. Is an idiot (with an idiot for an opponent) more likely to win with move A or move B? Those simulated games will give you the answer. Here’s the amazing thing: the idiot’s best move is your best move too. Don’t ask one clever mouse to solve the maze. Release ten thousand stupid mice and follow the lucky ones. This is what cheap computation buys you.
What’s beautiful about this approach is that it’s completely free of strategy. You don’t need to build up special knowledge structures about any particular game. You just need to know what moves are legal and how the game ends.
TIC TAC TOE
As soon as I read about this technique, I wanted to try it in MATLAB. So let’s make a program that can play Tic Tac Toe (also known as Naughts and Crosses). I’ve written Tic Tac Toe programs in MATLAB before. I’ve tried to make them clever and I’ve tried to make them learn. It’s not that hard. What’s fun about this Monte Carlo approach is that, with minimal effort I can teach it a new game. In fact, it makes playing lots of games easy. With a little object-oriented programming, you can write a generic game-playing harness. Then you just need to plug in some code that knows a few rules, and presto! You’ve got an instant game-playing program.
Here’s what I did. I made a class called TicTacToe that knows the rules of the game and how to draw the board. Then I wrote a function called botMoves that can look at the game object and make the next move. The separation is very clean. All of the Monte Carlo logic mentioned above lives in botMoves.
I only need a short script to have the bot play itself.
game = TicTacToe;
nSimulatedGames = 1000;
while ~game.isGameOver
botMoves(game,nSimulatedGames);
end
The variable nSimulatedGames refers to the number of simulated games we’ll ask our idiot friends to play for each potential move. Here’s an animation of what it looks like in action.
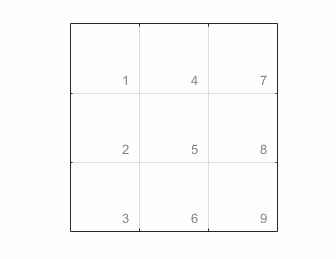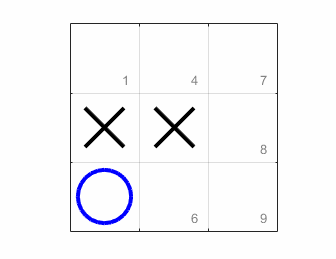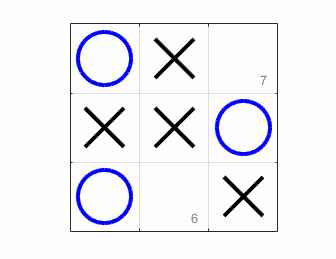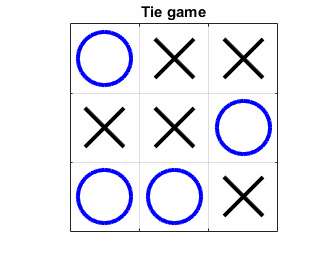
As it happens, the computer always ties itself. That’s actually good news, since Tic Tac Toe is unwinnable if your opponent is the least bit clever. So our bot is smart enough to prevent itself from winning. A little play-testing shows that it’s smart enough to avoid losing to a human too. But if we prefer, we can make the program less competitive by lowering the number of simulated games it plays. If I only let it run ten simulated games for each possible move, I can beat it easily.
I haven’t displayed much of my code here in the blog, but you can get your hands on it at this GitHub repository: Monte-Carlo-Games. Here is the TicTacToe class, and here is the botMoves function.
NEXT WEEK
This is the first of a two-part post. Next time we’ll show how quickly we can adapt our simple Tic Tac Toe harness for other games. We’ll also bring a community element into our programming. We’ll use Cody to source some of the tricky parts of our coding effort!






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.