Robot quickly teaches itself to walk using reinforcement learning
A team of researchers from the University of Southern California’s Valero Lab built a relatively simple robotic limb that accomplished something simply amazing: The 3-tendon, 2-joint robotic leg taught itself how to move. Yes, autonomous learning via trial and error.
The team was led by Professor Francisco Valero-Cuevas and doctoral student Ali Marjaninejad. Their research was featured on the cover of the March issue of Nature Machine Intelligence.
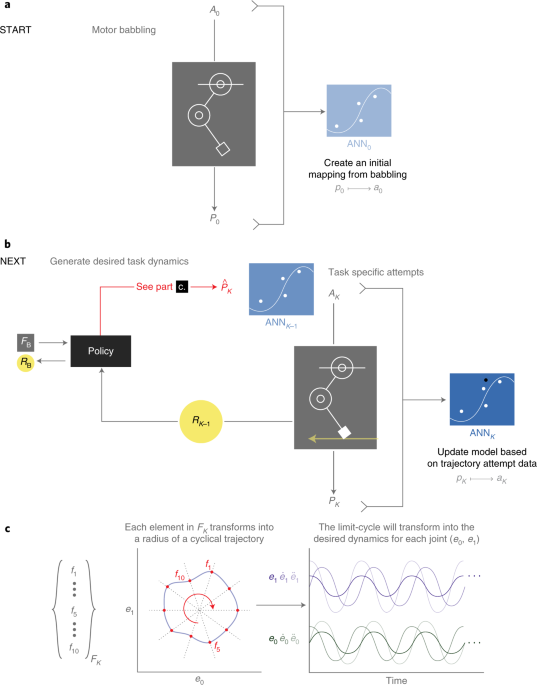
The robotic limb is not programmed for a specific task. It learns autonomously first by modeling its own dynamic properties and then using a form of artificial intelligence (AI) known as reinforcement learning. Instead of weeks upon weeks of coding, the robotic leg is able to teach itself to move in just minutes.
Inspired by nature
Roboticists have long been inspired by nature, since, let’s face it, Mother Nature has spent a long time perfecting her designs. Today, we see robots that walk like spiders and underwater robots inspired by sea snakes.
Bioinspiration also affects the way robots “think,” thanks to AI that mimics the way living organisms’ nervous systems process information. For example, artificial neural networks (ANNs) have been used to copy an insect’s brain structure to improve computer recognition of handwritten numbers.
For this project, the design took its cues from nature, both for the physical design of the leg and for the AI that helped the leg “learn” to walk. For the physical design, this robotic leg used a tendon architecture, much like the muscle and tendon structure that powers animals’ movements. The AI also took its inspiration from nature, using an ANN to help the robot learn how to control its movements. Reinforcement learning then utilized the understanding of the dynamics to accomplish the goal of walking on a treadmill.
Reinforcement learning and “motor babbling”
By combining motor babbling with reinforcement learning, the system attempts random motions and learns the properties of the system through the results of the motions. For this research, the team began by letting the system play at random, or motor babble, to learn the properties of the limb and its dynamics.
In an interview with PC Magazine, Marjaninejad stated, “We then give [the system] a reward every time it approaches good performance of a given task. In this case, moving the treadmill forward. This is called reinforcement learning as it is similar to the way animals respond to positive reinforcement.”
The resulting algorithm is called G2P, (general to particular). It replicates the “general” problem that biological nervous systems face when controlling limbs by learning from the movement that occurs when a tendon moves the limb. It is followed by reinforcement (rewarding) the behavior that is “particular” to the task. In this case, the task is successfully moving the treadmill. The system creates a “general” understanding of its dynamics through motor babbling and then masters a desired “particular” task by learning from every experience, or G2P.
The results are impressive. The G2P algorithm can learn a new walking task by itself after only 5 minutes of unstructured play and then adapt to other tasks without any additional programming.
The ANN uses the results from the motor babbling to create an inverse map between inputs (movement kinematics) and outputs (motor activations). The ANN updates the model based on each attempt made during the reinforcement learning phase to hone-in on the desired results. It remembers the best result each time, and if a new input creates a better result, it overwrites the model with the new settings.
Generating and training of ANNs was carried out using MATLAB and the Deep Learning Toolbox. The MATLAB code is available on the teams’ GitHub. The reinforcement learning algorithm was also written in MATLAB. A video of the robotic leg and the training results can be seen below.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.