加速度センサーの謎 加速度?ちから?重力?
こんにちは。今回は、以前「Simulink Desktop-Real-Timeの実力」というタイトルで記事を書いていただいた “toshi | Simulink の中の人” さんに再びゲスト投稿をしていただきます。前回は技術的にとても深い話で読者を魅了してくれましたが、今回もなんとも謎めいたタイトルで楽しみです。
===============
お久しぶりです。アプリケーションエンジニアリング部の toshi | Simulink の中の人です。今回も単発ゲストブロガーとして、記事を書かせていただきます。どうぞ宜しくお願い致します。
加速度センサー
加速度センサーとは、その名の通り、加速度を測るセンサーです。昨今流行りの自律ロボットや自動運転車、UAVなどにも搭載されています。用途としては、力学的な運動を計測する、重力の方向を調べる、などがあります。
加速度センサー初心者の方は「重力?」となるかもしれませんが、実は加速度センサーは、加速度と同時に重力も測っています。最初に、簡単に加速度センサーの原理について紹介します。加速度センサーにはいろいろな方式のものがありますが、ここでは、よく使われているMEMSの静電容量検出方式の紹介をします。
古典力学のニュートンの法則から、ばねに力が加わると、その力に比例した変位が発生します。したがって、その変位を測ればかかった力が分かるということです。そして、その変位を測定するために静電容量の測定を行います。
電極間距離が変化すると、静電容量が変化します。ということは、可動する電極にばねを取り付け、以下のように構成すれば完成します。結構簡単ですね。

静電容量から力に換算し、力から加速度に換算します。これで分かるように、加速度センサーは、結局「力」を測っているということです。なので、加速度も重力も同時に測れているわけですね。
それではここで、実際の加速度センサーの挙動を見てみましょう。今回は、教育向けの便利なマイコンボード「micro:bit」を使います。micro:bitには3軸加速度センサーが、それぞれx, y, z軸方向についています。それぞれの軸がマイコンボードのどっち方向なのか、については、画像よりも動画で見た方が早いかと思います。以下の動画を確認してください。
micro:bitをPCに接続し、Simulinkに信号を渡しています。acc_x, acc_y, acc_zはそれぞれ加速度センサーのx, y, z軸の値で、単位は[m/s^2]です。動画の方の解像度やフレームレートが悪く、動かしている時の様子が見づらいですが、(申し訳ありません安物Webカメラでして)それでも、何をしているかは分かると思います。
最初の静止している時は、z軸が上を向いており、平均的には (x, y, z) = (0, 0, 9.8) となっています。次にx軸を下に向けます。このとき、(x, y, z) = (-9.8, 0, 0) となります。つまり、重力は鉛直下向きに1Gに相当する大きさのベクトルとして計測されており、センサーの姿勢によって、3軸それぞれにその重力ベクトルの成分が現れることになります。
次に動かしている所を見てみると、重力成分はそのまま存在しており、それに加えて動かしたことによる加速度も現れます。この実際の動きに対する加速度の発生の仕方は、イメージ通りの波形かと思います。
センサーのモデル化
MATLABとSimulinkは知っての通り、シミュレーションツールです。最近は自動運転など、複雑なシステムでも丸ごとシミュレーションモデル化できるように、様々なことができるようになってきています。加速度センサーも、実はすでにモデル化されており、Aerospace Blocksetのライブラリに登録されています。ただしここでは、単にそれを使うのではなく、皆さんの理解を深めるため、敢えて自作することを検討します。モデルの理解は、例えば加速度センサーを使った状態推定など、アルゴリズムを構築する場合にとても重要になります。
モデルとは、すなわち計算式です。結論から言いますが、加速度センサーの計測値(acc_x, acc_y, acc_z)は、以下の式で求めることができます。

fは重力以外のセンサーにかかっている力の合成ベクトル、mは質量(スカラー)です。fの中には、回転運動によって生じる遠心力なども含まれます。Rはセンサーの3次元の姿勢を表す3×3回転行列です。回転行列は、ベクトルにかけることで、そのベクトルを3次元回転させることができます。これにより、地上に固定された座標系のベクトルであるf/mを、センサーの座標系に変換することができます。
ここまでの話で、皆さんが気になっている所は分かります。上記の「重力以外」とは一体どういうことなのでしょうか。最初に「加速度センサーは重力ベクトルを測る」と言っておきながら、重力を無視するとはどういうことでしょうか。理解の促進のために、次は数式ではなく、図で説明してみます。以下の図は、加速度センサーモデルの一例です。

センサーの座標系は地上の座標系と一致しているとします。よってRは単位行列となります。次に、机からの抗力と指から加わる力を加算し、質量mで割ります。結果、図のように(acc_x, acc_y, acc_z) = (1, 0, 9.8)となります。
これで分かりましたでしょうか? 分かった人はもうこのページを閉じて構いません。分からなかった人は、以下を続けて読みましょう。
重力とは
違和感の正体は「かかっている力の中で、なぜ重力だけを省く必要があるのか」だと思います。しかし、その違和感とは裏腹に、上記の動画を見ると、実際そのように動作していることがわかります。
ここで、以下のような状況を考えてみてください。道を歩いていたあなたは、突然麻酔薬を打たれて昏倒し、拉致されます。目を覚ますと、今まで訪れたことのない部屋に監禁されています。その部屋には外の様子を確認できる窓がありません。この状況であなたは、以下の図のA, B どちらの状況に置かれているか、判断することができますでしょうか。
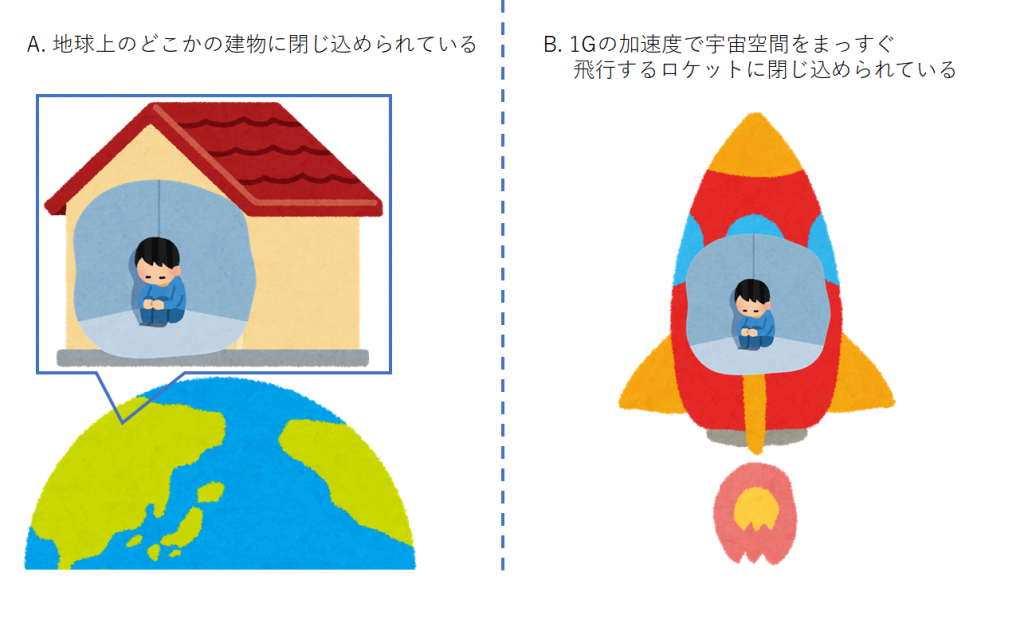
答えは「できない」です。しかも、仮にあなたが加速度センサーを持っていたとしても、A, Bどちらであるかを知る術はありません。なぜなら、そもそも重力というのは存在していないからです。したがって、A, Bは両方とも物理的には同一の事象です。(厳密には、磁気や放射線のパターンが地球上と宇宙空間では異なるので、それらを測定すれば分かりますが、今回は考慮しません。)
Aには重力が存在していて、Bには存在していない。そう感じてしまうのが一般的な感覚ですが、マクロな物理現象をより正確に分析すると、実は間違いであることがわかります。重力というのは、正しくは「重力場によって物体が動く際に見える、見かけの力」のこと言います。地球の近傍の物体は、重力を受けて1Gの加速度で地球の中心に落下しているように見えますが、実はそうではありません。地球近傍の重力場の中で静止している、というのが正しいのです。一方、地表に立っている人、または机の上の加速度センサーは、地面から力を受けて、1Gの加速度で常に加速しているのです。
その証拠に、自由落下している加速度センサーは、(acc_x, acc_y, acc_z) = (0, 0, 0) を計測します。以下の動画をご確認ください。
カメラの画角が狭く、落下は一瞬しか捉えられていませんが、確かに0に近くなっていることがわかると思います。
不思議な話で中々受け入れられないかもしれませんが、これはれっきとした物理の理論です。そう、アインシュタインの一般相対性理論そのものですね。ニュートンの運動方程式は、一般相対性理論の測地線の方程式の近似です。より正しくは、測地線の方程式と重力場の方程式から物理現象を捉える必要があります。
結局、加速度センサーは何を測っているのか
もちろん、加速度センサーを工学の用途で用いることにおいて、一般相対性理論を扱えるようになる必要はありません。なぜなら、我々が活動している空間においては、ニュートン力学は一般相対性理論の近似として、十分に精度が良いからです。(それに、測地線・重力場の方程式のような大規模な計算は、できる限り避けたいです。)ただし、重力の計測に関する謎を理解するためには、一般相対性理論の概念を理解する必要があったわけです。
結局のところ、”センサーのモデル化”の節で述べた式を理解していれば大丈夫です。要点をまとめると、結局こういうことです。
「加速度センサーは重力を測る」というのは間違いです。そもそも重力というものは存在しません。加速度センサーは力を測っています。その力は相対論的な力です。もし、ニュートン力学に近似できる物理領域かつ地球近傍での計測において、我々が思っている加速度を知りたい場合は、「地表に留まるために加えられている力」を「かかっている全ての力」から引いた力から、加速度に換算する必要があります。
このことを理解して貰えれば、今日の話は終わりです。一般相対性理論なんて、難しすぎて理解できないし、何より自分と縁なんて無いと思ってませんでした? 実は結構身近に存在しているんですよ。量子力学もそうです。パソコンやスマホが計算するために使っている「半導体」という現象も、量子力学の理論から説明することができます。意外な所から出てきた一般相対性理論ですが、もし興味を持った方がいましたら、是非勉強してみてください。きっと新しい世界を見ることができると思います。
- カテゴリ:
- 機能と使い方



コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。