Simscape モデルから運動方程式を導出してみる〜ブロックのソースコードを読み解く〜
今回はテクニカルコンサルティング部の本郷がお送りします。
—
はじめに
こんにちは。テクニカルコンサルティング部の本郷です。前回のブログでは、Simscapeにおける「アクロス変数」と「スルー変数」について解説しました。
今回は、それらの保存則を適用し、Simscapeモデルから運動方程式を導出してみます。
言い換えると、Simscapeが内部で自動生成している方程式の構築プロセスを手作業で再現し、その仕組みをより深く理解することを目指します。
ただし、厳密にやると数式が煩雑になるため、今回は本質が伝わる程度に簡略化して解説します。
マス・バネ・ダンパ系のSimscapeモデル
今回扱うのは、以下の図1に示すようなマス・バネ・ダンパ系のSimscapeモデルです。 これはMathWorksの公式ドキュメントにあるモデルを少し書き換えたものです。マス・バネ・ダンパの各要素が視覚的に接続されており、前回のブログで述べた「直感的なモデリング」が可能であることが分かります。

準備
運動方程式を導出する前に、いくつかの準備をしておきましょう。
図1にその内容を示しています。
ノードの命名
図1には二箇所にノードがあり、それぞれに名前を付けておきます。右側を「ノード1」、左側を「ノード2」とします。
なお、左側にはノードが2つあるように見えますが、これらは接続されているため、実質的には1つのノードとみなせます。
アクロス変数(速度)
- スプリングブロックのアクロス変数(速度)を $ v_1 $
- ダンパブロックのアクロス変数を $ v_2 $
と定義します。これらは、それぞれのブロックにおけるCノードとRノード間の速度差です。
スルー変数(力)
ノード1におけるスルー変数は、図1のように定義します。
ノード1から各ブロックに向かう方向を正とし、スプリング、ダンパ、マスにかかる力をそれぞれ $ F_1 $, $ F_2 $, $ F_3 $ とします。
アクロス・スルー変数の保存則(おさらい)
ここで、アクロス・スルー変数の保存則を簡単におさらいしておきます。
|
変数
|
保存則
|
|
アクロス変数
|
ループを形成するアクロス変数の和はゼロ、またはノード間のアクロス変数は等しい。
|
|
スルー変数
|
1つのノードに流れ込むスルー変数の総和はゼロ。
|
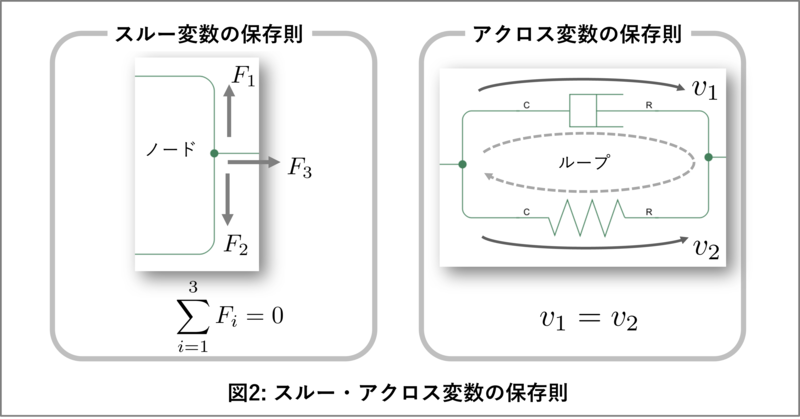
これらの保存則を図2にまとめました。左側がスルー変数、右側がアクロス変数の保存則です。
各要素の方程式
それでは方程式を導出を開始しましょう。大雑把な流れは次の通りです:まず要素の方程式を確認します。次にそれらに保存則を適用します。そして、最終的な運動方程式を導出します。
マス・バネ・ダンパ系を構成する各要素の方程式を以下に示します。
それぞれのブロックにおける物理量(変位、速度、力)には、順に添字を付けて整理しています。
バネ(Translational Spring ブロック)
皆さんはSimscapeブロックのソースコードを確認したことがありますか?すべてではないですが、多くのSimscapeブロックは内部のソースコードを確認できます。
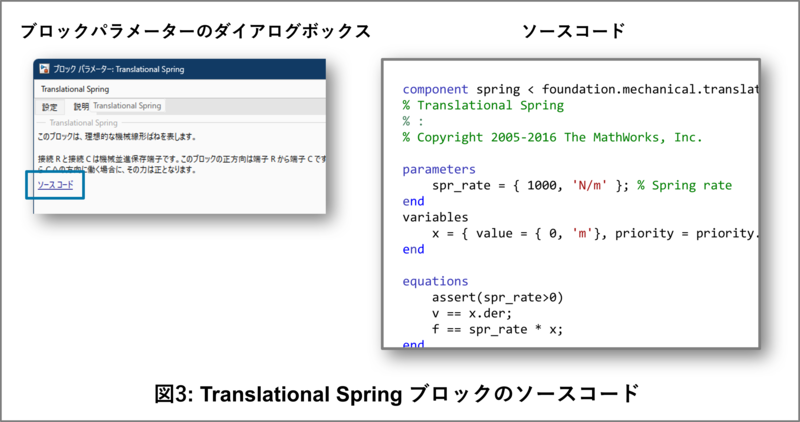
確認方法は、まずブロックをダブルクリックしてブロックパラメーターのダイアログボックスを開きます。次に説明タブにあるソースコードのリンクをクリックします。するとソースコードがMATLABでオープンされます。図3にバネ(Translational Spring)ブロックのソースコードのリンクとソースコードの例を示してあります。
ソースコードのequations構文を引用します:
equations
assert(spr_rate>0)
v == x.der;
f == spr_rate * x;
end
ソースコードはSimscape言語で記述されています。Simscape言語は、物理モデリングのためにMATLAB言語を拡張した固有言語であり、ブロックの動作を記述するために使用されます。上の例で、.derは時間微分を、== は代入ではなく「等しい」を表現しています。fは力(スルー変数)、vは速度(アクロス変数)、xはバネの変位、spr_rateはバネ定数です。
このソースコードから、このブロックの方程式を書き出していきます。人間が読みやすいように物理変数は一般的な表記に書き換えています。バネの力$ F_1 $は、バネ定数 k と変位量 $ x_1 $ の積で表されます:
$ F_1 = k \cdot x_1 $
$ v_1 = \dot{x}_1 $
変位$ x_1 $の時間微分が速度$ v_1 $ です。 これは一般的によく知られたバネの方程式です。
ノードは C1, R1 とし、$ v_1 = \mathrm{R1}.v – \mathrm{C1}.v $ と定義します。この関係は上記のソースコードには直接記載されていません。どこに記載されているかと言うと、このブロックが継承しているfoundation.mechanical.translational.branchに記載されています。
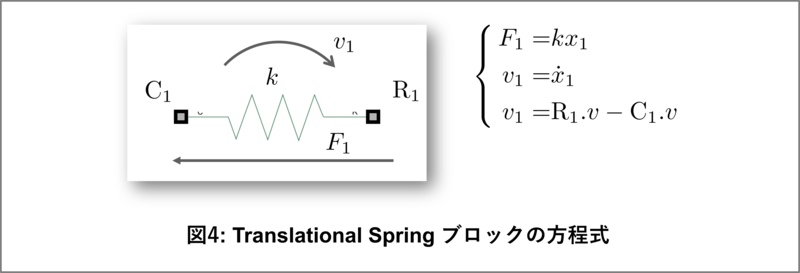
図4にバネ(Translational Spring)ブロックのポート、およびアクロス・スルー変数と方程式をまとめてあります。
ダンパ(Translational Damper ブロック)
次はダンパの方程式です。バネと同様にブロックのソースコードの一部を引用します:
equations
f == b * v;
v == R.v – C.v;
end
f, vはバネと同様、bは減衰係数です。このブロックはfoundation.mechanical.translational.branchを継承していないため、アクロス変数vとノードでのアクロス変数の関係が直接記述されています。
減衰係数の記号bを一般的な表記のcに変更して、以下のような方程式を書き出すことが出来ます。ダンパの力$ F_2 $は、減衰係数 c と速度 $ v_2 $ の積です:
$ F_2 = c \cdot v_2 $
ノードは C2, R2 とし、$ v_2 = \mathrm{R2}.v – \mathrm{C2}.v $ と定義します。
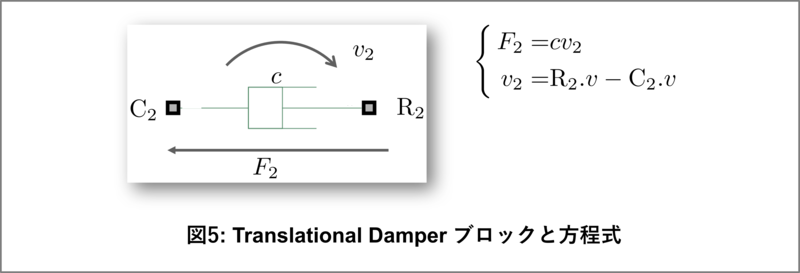
図5にダンパ(Translational Damper)ブロックのポート、およびアクロス・スルー変数と方程式をまとめてあります。
マス(Mass ブロック)
このブロックはノードが1つ(M)だけという点で少し特殊です。ソースコードの一部を引用します:
equations
f == mass * v.der;
v == M.v;
end
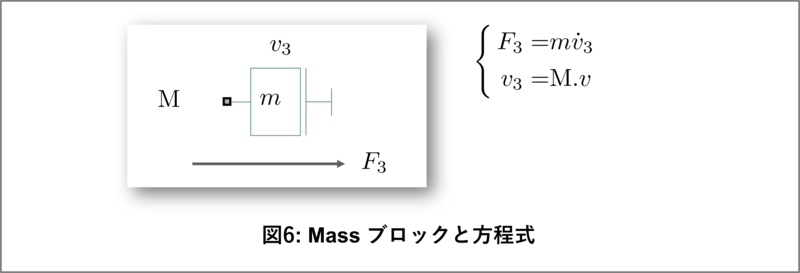
質量massを一般的な表記のmに変更して、以下のように運動方程式を書き出します。マスの運動方程式は、質量 m と加速度 $ \dot{v}_3 $ の積が力 $ F_3 $ に等しいという、ニュートンの法則です:
$ F_3 = m \cdot \dot{v}_3 $
ノードMにおける速度は $ \mathrm{M}.v = v_3 $ です。
図6にマス(Mass)ブロックのポート、およびアクロス・スルー変数と方程式をまとめてあります。
リファレンス(Mechanical Translational Reference ブロック)
このブロックも特殊で、以下の2点が特徴です:
1. ノードが1つ(V)だけ
2. 座標の原点を定義する
ソースコード(一部)は以下のようになっています:
connections
connect(V, *);
end
他のブロックと違ってequationsの構文がなくconnectionsの構文のみです。connections は、ノード間の接続を定義するもので、connect(V, ); は、ノード V をグローバルな機械的基準点に接続することを意味します。* は Simscape における「物理的基準点(ground)」を表す特殊な記号です。これにより、V は動かない絶対的な基準点として機能します。何の基準かというと、アクロス変数の基準です。
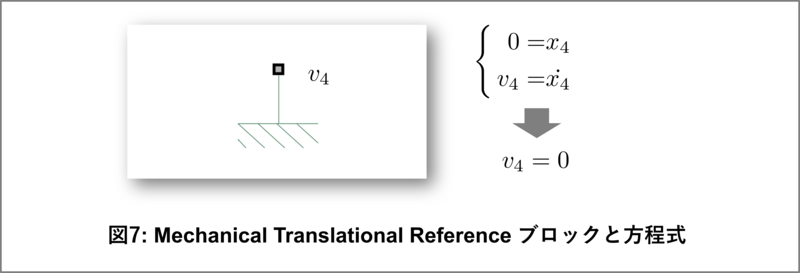
表記を分かりやすくするためにノードVのアクロス変数を$ v_4 $とします。こうすると変位 $ x_4 = 0 $ 、速度 $ v_4 = 0 $ となります。
図7にリファレンス(Mechanical Translational Reference)ブロックのポート、およびアクロス変数と方程式をまとめてあります。
アクロス変数の保存則の適用
アクロス変数の保存則は、次のようにも言い換えられます:
> 「各ノードに接続されたすべてのブロックにおいて、そのノードにおけるアクロス変数の値は等しい」
この保存則をノード1とノード2に適用し、式を導出します。これを図8に示しました。
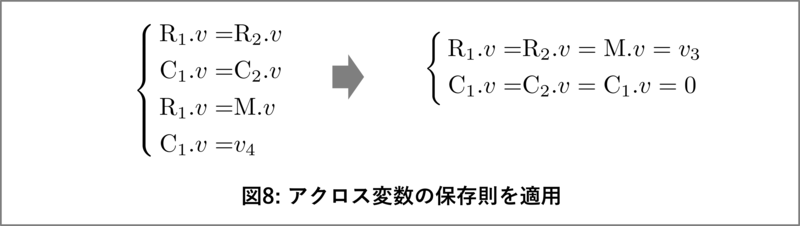
変数を整理して、各ブロックの方程式を簡潔に書き直すと、数式がかなりすっきりします。図9に各ブロックの方程式を書き直した結果を示しました。

全体の運動方程式
最後に、スルー変数の保存則を使って全体の運動方程式を構築します。
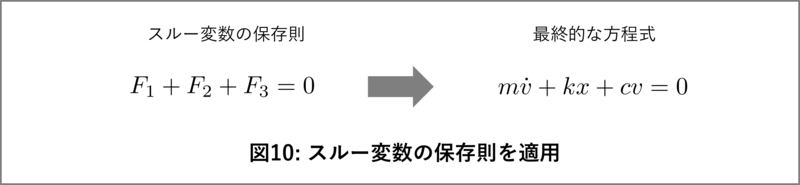
ノード1におけるスルー変数の保存則を適用し、$ F_1, F_2, F_3 $ をそれぞれの式に代入すると、
$ F_1 + F_2 + F_3 = 0. $
となります。この$ F_1, F_2, F_3 $にそれぞれ図9にある各ブロックの方程式を代入することで、最終的に以下のような、よく知られたマス・バネ・ダンパ系の運動方程式が得られます。図10に最終的な方程式を示しました。
応用編
ここまでの例は外力が存在しない場合です。実際のモデリングでは外力が存在するケースが一般的です。外力がある場合は、モデルにIdeal Force Sourceを追加します。具体的には図1のモデルのノード1にIdeal Force Source のR端子を接続し、C端子をReferenceに接続します。
この際、スルー変数である力の向きはC→Rが正になります。これはMechanicalドメインのSourceブロックに共通で、Rから外に出る向きが力の正やトルクになります。この外力をFとすると、最終的な方程式はよく知られた強制振動の式
$ F_1+F_2+F_3 = F $
になります。ぜひ御自身で導出を試してみて下さい。
おわりに
今回は、Simscapeモデルから運動方程式を導出するという、少しマニアックな試みをご紹介してみました。
Simscapeが内部でどのように方程式を構築しているのか、その雰囲気を感じ取っていただけたら嬉しいです。上の例ではマス・バネ・ダンパ系という最も単純な系を題材にしたので手動でなんとかトレースできます。系が複雑になると方程式と変数が増えていきますから手動で方程式を導出するのはハードルが上がります。なお、Simscape言語に関しては公式のドキュメントがあります(Simscape 言語入門)。
数値計算の観点では、変数が増えるとそれだけ計算量が増えます。Simscapeはブロックを並べることで直感的なモデリングが可能ですが、必要以上に計算量が多くなっていないか注意が必要です。モデリングはまず単純な系から始めて、必要に応じて忠実度を向上させることが重要です。モデリング対象の規模が大きくなると、この重要度は増していきます。



Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.