Sean‘s pick this week is polygon2voxel by Dirk-Jan Kroon.

I was recently asked: “How can you find the intersecting volume of two polyhedra?”

R2017b introduced polyshape to MATLAB to make working with two dimensional polygons easy. However, it does not support 3D.

One way to get an approximation to the volume would be to convert the polyhedra to a three dimensional image and find the overlapping voxels. Dirk-Jan’s polygon2voxel helps with the first step of this.

First, let’s create two 3D shapes, one convex, and one not.

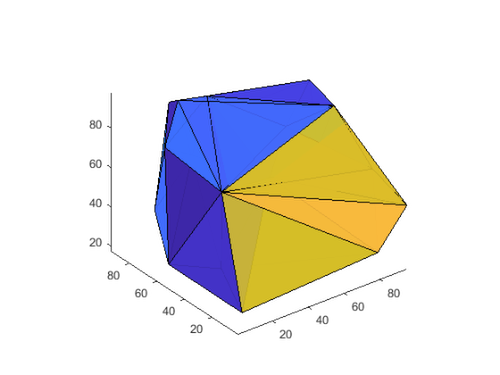
xyz = gallery('uniformdata', [30 3], 0)*100;
DT = delaunayTriangulation(xyz);
figure
tetramesh(DT)

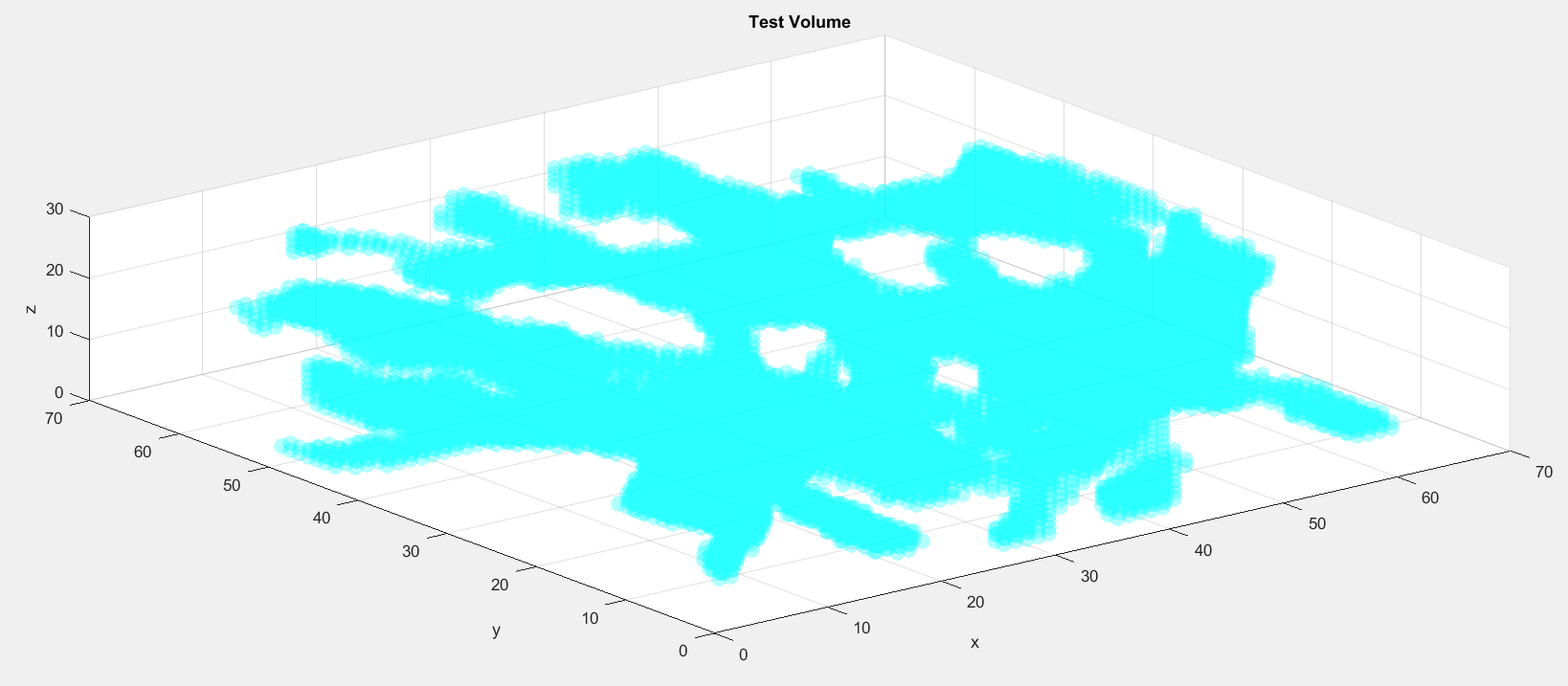
xyz = gallery('uniformdata', [30 3], 1)*100;
AS = alphaShape(xyz, 40);
figure
plot(AS)

Now let’s convert these to voxels. I will use just the freeBoundary, i.e. the surface, of the delaunay triamgulation.

[f, t] = freeBoundary(DT);
ConvexImage = polygon2voxel(struct('faces', f, 'vertices', t), [100 100 100], 'auto');

For an alphaShape, boundaryFacets will return the surface.

[f, t] = boundaryFacets(AS);
ConcaveImage = polygon2voxel(struct('faces', f, 'vertices', t), [100 100 100], 'auto');

We can watch both volumes as a movie.

implay([ConvexImage ConcaveImage])

The holes in the volumes have not been filled; imfill can do that for us.

ConvexImage = imfill(ConvexImage, 'holes');
ConcaveImage = imfill(ConcaveImage, 'holes');

implay([ConvexImage ConcaveImage])

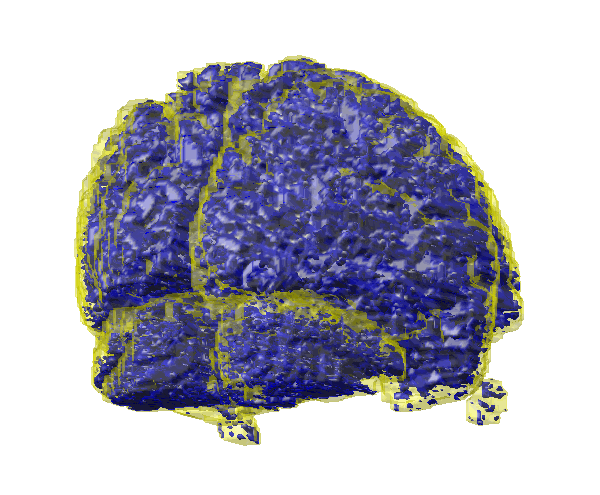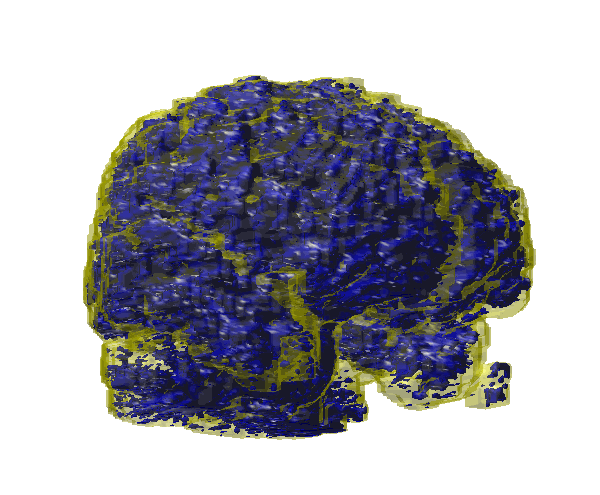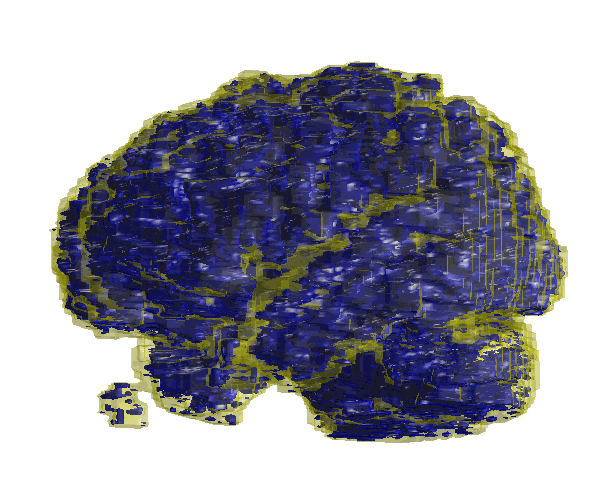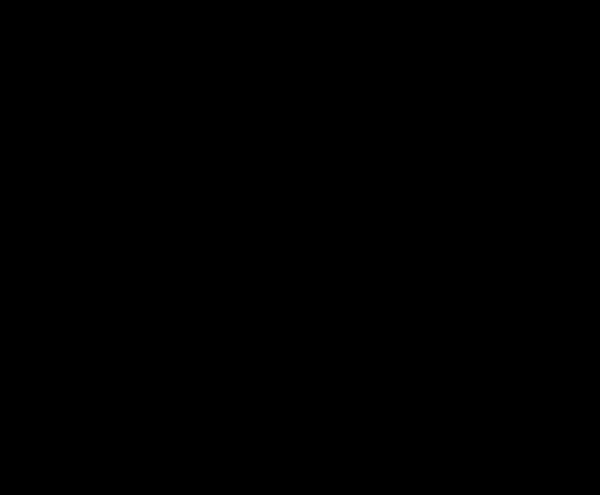
Now logical indexing can be used to find the overlapping volume:

VoxelIntersection = ConvexImage & ConcaveImage;
figure
isosurface(VoxelIntersection)

The volume could be computed as just the sum of the voxels:

volumevoxels = sum(VoxelIntersection, 'all');
disp("The intersecting volume is: " + volumevoxels + "units")

The intersecting volume is: 272741units

Comments

Do you have a use case for 3D polyshapes in MATLAB? Give it a try and let us know what you think here or leave a comment for Dirk-Jan.

Published with MATLAB® R2019b