Aliasing and the discrete-time Fourier transform
Many of you were onto me immediately last week. I asked you to estimate the frequency of the sampled cosine signal below, and readers quickly chimed in to guess that this question was really a teaser about aliasing.
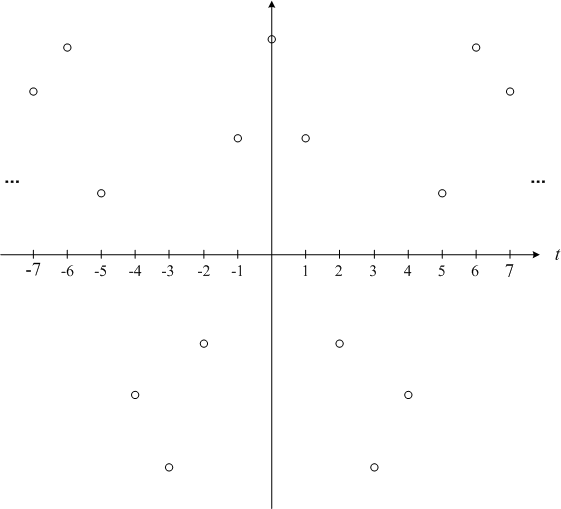
As it happened, I started with a 1 rad/second cosine,  ,
,  :
:
t = linspace(-2.3*pi, 2.3*pi, 800);
alpha = 1;
x_c = cos(alpha * t);
plot(t, x_c, 'k')
And I sampled that signal to get  with
with  so that
so that  .
.
T = 1; n = -7:7; nt = n * T; x = cos(alpha*n*T); hold on plot(nt, x, 'ok') hold off

But I could have started with a completely different frequency and still ended up with exactly the same samples. For example, let's see what happens when we try  :
:
alpha_2 = 2*pi - 1; x2_c = cos(alpha_2 * t); plot(t, x2_c, 'k') x2 = cos(alpha_2 * n * T); hold on plot(nt, x2, 'ok') hold off

The two sets of samples are the same (within floating-point round-off error):
max(abs(x - x2))
ans = 1.1657e-015
Let's look at this phenomenon in terms of the relationship between the continuous-time Fourier transform and the discrete-time Fourier transform (DTFT). Below is the continuous-time Fourier transform of  .
.

The DTFT is a collection of copies of the continuous-time Fourier transform, spaced apart by the sampling frequency, and with
the frequency axis scaled so that the sampling frequency becomes  . Here's the DTFT of
. Here's the DTFT of  .
.

Now  has a higher frequency as you can see in the plot of its continuous-time Fourier transform:
has a higher frequency as you can see in the plot of its continuous-time Fourier transform:

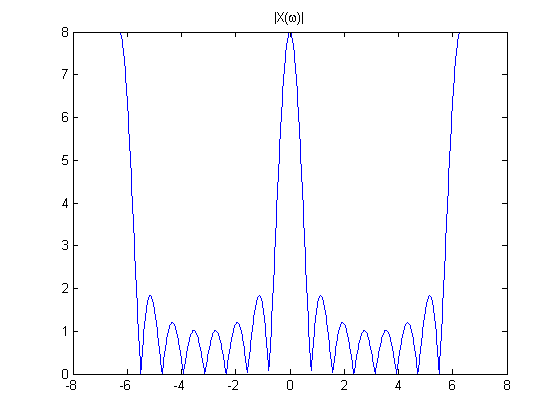
But when you make a bunch of copies of  spaced apart by the sampling frequency, you find that the DTFT of
spaced apart by the sampling frequency, you find that the DTFT of  is exactly the same as the DTFT of
is exactly the same as the DTFT of  .
.

Usually only a single period of the DTFT is plotted:

In other words, when you use a sampling rate of  , the frequencies 1 and
, the frequencies 1 and  are indistinguishable. This is called aliasing. In general, the continuous-time frequency
are indistinguishable. This is called aliasing. In general, the continuous-time frequency  is indistinguishable from any other frequency of the form
is indistinguishable from any other frequency of the form  , where
, where  is an integer.
is an integer.
So far we've talked about the continuous-time Fourier transform, the discrete-time Fourier transform, their relationship, and a little bit about aliasing. Next time we'll bring the discrete Fourier transform (DFT) into the discussion. That's what the MATLAB function fft actually computes.
- Category:
- Fourier transforms
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building





Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.