The DFT and the DTFT
It's finally time to start looking at the relationship between the discrete Fourier transform (DFT) and the discrete-time Fourier transform (DTFT). Let's look at a simple rectangular pulse, ![$x[n] = 1$](https://blogs.mathworks.com/images/steve/2010/dft_samples_dtft_eq33869.png) for
for 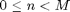 . The DTFT of
. The DTFT of ![$x[n]$](https://blogs.mathworks.com/images/steve/2010/dft_samples_dtft_eq17606.png) is:
is:
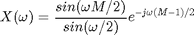
Let's plot 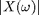 for
for 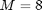 over a couple of periods:
over a couple of periods:
M = 8;
w = linspace(-2*pi, 2*pi, 800);
X_dtft = (sin(w*M/2) ./ sin(w/2)) .* exp(-1j * w * (M-1) / 2);
plot(w, abs(X_dtft))
title('|X(\omega)|')
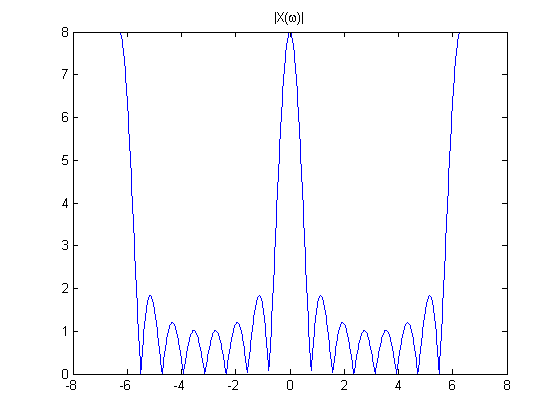
It turns out that, under certain conditions, the DFT is just equally-spaced samples of the DTFT. Suppose ![$X_P[k]$](https://blogs.mathworks.com/images/steve/2010/dft_samples_dtft_eq88255.png) is the P-point DFT of
is the P-point DFT of ![$x[n]$](https://blogs.mathworks.com/images/steve/2010/dft_samples_dtft_eq17606.png) . If
. If ![$x[n]$](https://blogs.mathworks.com/images/steve/2010/dft_samples_dtft_eq17606.png) is nonzero only over the finite domain
is nonzero only over the finite domain 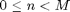 , then
, then ![$X_P[k]$](https://blogs.mathworks.com/images/steve/2010/dft_samples_dtft_eq88255.png) equals
equals 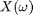 at equally spaced intervals of
at equally spaced intervals of  :
:
![$$X_P[k] = X(2\pi k/P),\ k=0, \ldots, P-1$$](https://blogs.mathworks.com/images/steve/2010/dft_samples_dtft_eq68762.png)
The MATLAB function fft computes the DFT. Here's the 8-point DFT of our 8-point rectangular pulse:
x = ones(1, M); X = fft(x)
X =
8 0 0 0 0 0 0 0
One 8 and a bunch of zeros?? That doesn't seem anything like the DTFT plot above. But when you superimpose the output of fft in the right places on the DTFT plot, it all becomes clear.
P = 8; w_k = (0:P-1) * (2*pi/P); X = fft(x); plot(w, abs(X_dtft)) hold on plot(w_k, abs(X), 'o') hold off
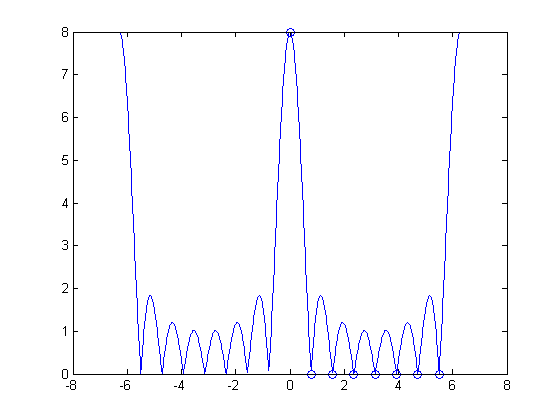
Now you can see that the seven zeros in the output of fft correspond to the seven places (in each period) where the DTFT equals zero.
You can get more samples of the DTFT simply by increasing P. One way to do that is to zero-pad.
x16 = [x, zeros(1, 8)]
x16 =
Columns 1 through 13
1 1 1 1 1 1 1 1 0 0 0 0 0
Columns 14 through 16
0 0 0
P = 16; X16 = fft(x16); w_k = (0:P-1) * (2*pi/P); X = fft(x); plot(w, abs(X_dtft)) hold on plot(w_k, abs(X16), 'o') hold off
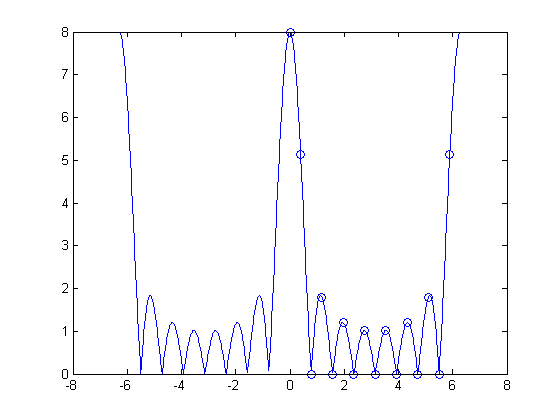
Another way to increase P is to use the fft(x,P) syntax of the fft function. This syntax computes the P-point DFT of x by using zero-padding. Let's try a 50-point DFT.
P = 50; Xp = fft(x, P); w_k = (0:P-1) * (2*pi/P); X = fft(x); plot(w, abs(X_dtft)) hold on plot(w_k, abs(Xp), 'o') hold off
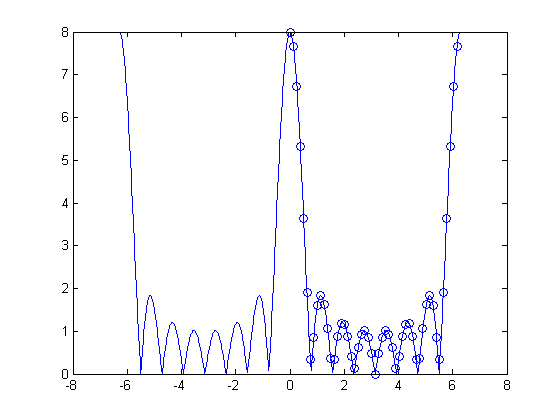
If you've ever wondered what that whole zero-padding business was all about with Fourier transforms, now you know. When you tack on a bunch of zeros to a sequence and then compute the DFT, you're just getting more and more samples of the DTFT of the original sequence.
I think the next logical place to go in our Fourier exploration is to start considering some of the reasons why many people find the output of fft so surprising or puzzling. Here's a sample:
- Why isn't the zero frequency (or "DC" frequency) in the center of the output from fft?
- Why isn't the output of fft real when the input is symmetric?
Do you have puzzles to add? Let me know by adding your comments.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building





Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.