Last month I was experimenting with an algorithm in which I needed to construct a set of equidistant steps along a path consisting of line segments. (I'll call this a polyline path, or polyline for short.) Today I want to show you how to construct such a path in MATLAB. Along the way I'll show you the function improfile and give you a pointer to a database of sample range images that I found.

Contents

Polylines

Here's a simple example of a polyline. (Note that, because we're going to be talking about distances, I'm going to set the aspect ratio of my plots to be 1:1 by calling axis equal.)

x = [24 214 327 617];
y = [375 223 218 341];
plot(x,y)
axis equal

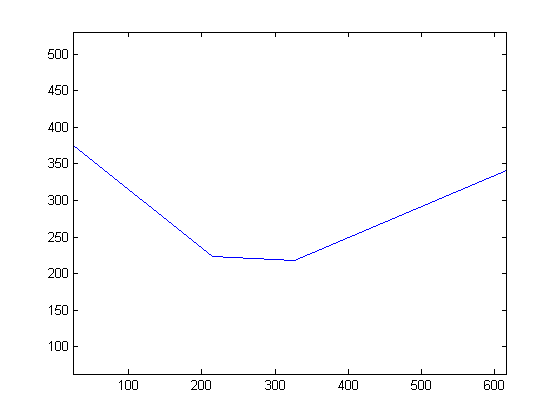
This has three connected line segments. In this example, each segment has a different length. I wanted to be able to find a certain number of points that were equally spaced along this path.

IMPROFILE

After pondering this problem for a minute or so, I remembered that the function improfile does exactly this computation internally. The function improfile is used to compute pixel-value profiles along a user-specified polyline.

Let me illustrate improfile using a range image. In a range image, the pixel values represent estimated distance from the imaging device. I found the USF (University of South Florida) Range Image Database online. Below is a range image I downloaded from the database. It was taken by the Vision Lab at USF using a "K2T structured light camera." (No, I don't know what that is.) The web site helpfully tells me that the image is stored in "rasterfile format," which is pretty dated but fortunately supported by imread.

url = 'https://blogs.mathworks.com/images/steve/2012/chessmen.range';
I = imread(url, 'ras');
imshow(I, 'InitialMagnification', 50)

Let's use improfile to compute a cross-section of range values along a particular path. First, though, let me superimpose the path on the image so you can where it is. (Although improfile has an interactive mode that lets you select the path using a mouse, I can't show that here.)

hold on
plot(x,y,'r','LineWidth',5)
hold off

Here's the cross-section of range values.

improfile(I,x,y)

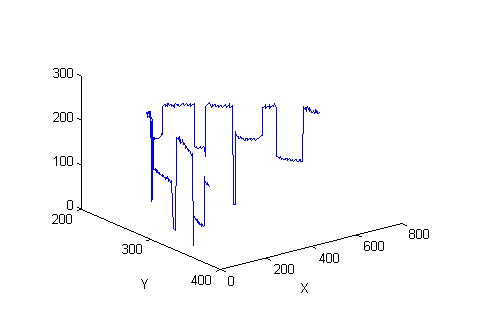
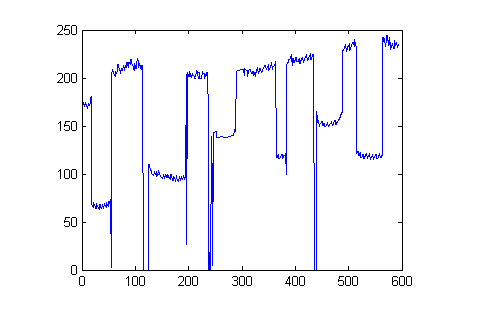
You can see that improfile shows the cross-section as a 3-D plot. To see the cross-section as a normal 2-D line plot, call improfile with an output argument to get the cross-section values and then pass them to plot.

c = improfile(I,x,y);
plot(c)

Computing equidistant steps along the polyline

As part of its computation, improfile needs to compute equidistant steps along the polyline path. So how does that work?

The function first computes the cumulative distance from the beginning of the polyline to each vertex along the way, and then it uses a clever call to interp1 to compute the steps.

xy = [x' y'];
d = diff(xy,1)

d =

   190  -152
   113    -5
   290   123

dist_from_vertex_to_vertex = hypot(d(:,1), d(:,2))

dist_from_vertex_to_vertex =

  243.3187
  113.1106
  315.0063

cumulative_dist_along_path = [0;
    cumsum(dist_from_vertex_to_vertex,1)]

cumulative_dist_along_path =

         0
  243.3187
  356.4293
  671.4356

Now we can get our steps by constructing a call to interp1.

num_points = 20;
dist_steps = linspace(0, cumulative_dist_along_path(end), num_points);
points = interp1(cumulative_dist_along_path, xy, dist_steps)

points =

   24.0000  375.0000
   51.5949  352.9241
   79.1898  330.8482
  106.7847  308.7722
  134.3796  286.6963
  161.9745  264.6204
  189.5694  242.5445
  218.0483  222.8209
  253.3525  221.2587
  288.6567  219.6966
  323.9609  218.1345
  356.7328  230.6108
  389.2662  244.4095
  421.7996  258.2081
  454.3330  272.0068
  486.8664  285.8054
  519.3998  299.6041
  551.9332  313.4027
  584.4666  327.2014
  617.0000  341.0000

Plot the points, superimposing them on the original path, to see how we did.

plot(x,y)
hold on
plot(points(:,1), points(:,2), 'o')
hold off
axis equal

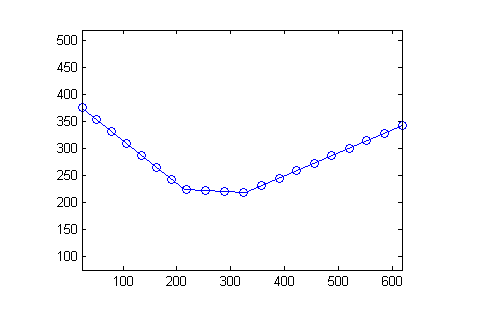
There you go. Now you know about improfile, you know how to compute a path along a polyline, and you know about an online database of sample range imagery.

I think we should call it a day.

Get the MATLAB code

Published with MATLAB® 7.14

Published with MATLAB® 7.14