Watershed transform question from tech support
A support call came in this week from a customer trying to use watershed to segment this image:

The complaint was that calling watershed did not produce a good segmentation.
Today I want to show how to use watershed to segment this image. Along the way I'll explain the difference between the watershed transform and watershed segmentation.
First, let's just try calling watershed and see what happens.
url = 'https://blogs.mathworks.com/images/steve/2013/blobs.png';
bw = imread(url);
L = watershed(bw);
Lrgb = label2rgb(L);
imshow(Lrgb)
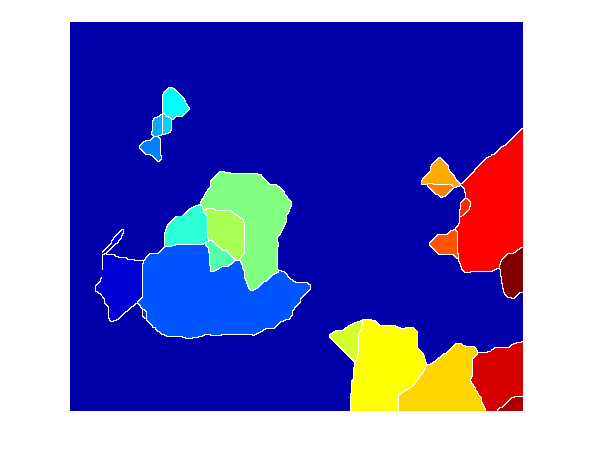
When I saw that result, I was puzzled at first. Then I realized what was going on. Let me use imfuse to show these two images together, zooming in on one particular blob.
imshow(imfuse(bw,Lrgb)) axis([10 175 15 155])

You see, the watershed transform always gives you one watershed region for every local minimum (or regional minimum) in the image. These little black "noise spots" are local minima, and so there's a watershed region around each one.
Even if we fill these holes, though, just using the watershed transform by itself is never going to produce the segmentation that the customer was seeking. That brings me to my point about the distinction between watershed segmentation and the watershed transform. Watershed segmentation refers to a family of algorithms that are based on the watershed transform. Except for very specific cases, the watershed transform isn't a full segmentation method on its own.
Some years ago, I wrote a MathWorks newsletter article called The Watershed Transform: Strategies for Image Segmentation. It's worth reviewing in order to brush up on the basics. An central concept from the article is this:
The key behind using the watershed transform for segmentation is this: Change your image into another image whose catchment basins are the objects you want to identify.
For an image such as this, consisting of roughly circular, touching blobs. the distance transform can be useful for producing an image whose "catchment basins are the objects you want to identify."
Before go to the distance transform, though, let's clean up the noise a bit. The function bwareaopen can be used to remove very small dots. It removes them in the foreground, though, so we complement the image before and after calling bwareaopen.
bw2 = ~bwareaopen(~bw, 10); imshow(bw2)

D = -bwdist(~bw); imshow(D,[])

Now we're starting to get somewhere. Next, compute the watershed transform of D.
Ld = watershed(D); imshow(label2rgb(Ld))
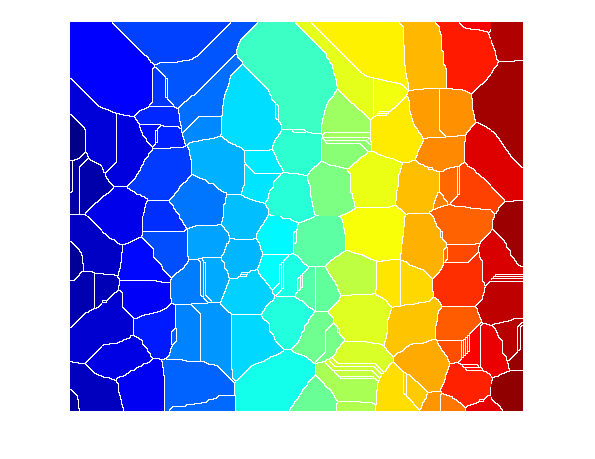
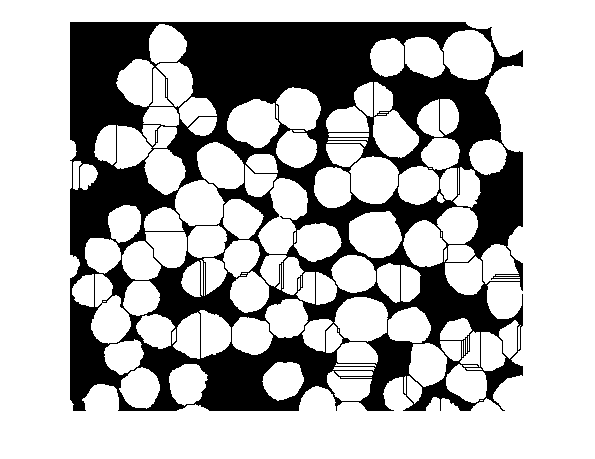
The watershed ridge lines, in white, correspond to Ld == 0. Let's use these ridge lines to segment the binary image by changing the corresponding pixels into background.
bw2 = bw; bw2(Ld == 0) = 0; imshow(bw2)
The "raw" watershed transform is known for its tendency to "oversegment" an image. The reason is something I mentioned above: each local minimum, no matter how small, becomes a catchment basin. A common trick, then, in watershed-based segmentation methods is to filter out tiny local minima using imextendedmin and then modify the distance transform so that no minima occur at the filtered-out locations. This is called "minima imposition" and is implemented via the function imimposemin.
The following call to imextendedmin should ideally just produce small spots that are roughly in the middle of the cells to be segmented. I'll use imshowpair to superimpose the mask on the original image.
mask = imextendedmin(D,2);
imshowpair(bw,mask,'blend')

Home stretch, now. Modify the distance transform so it only has minima at the desired locations, and then repeat the watershed steps above.
D2 = imimposemin(D,mask); Ld2 = watershed(D2); bw3 = bw; bw3(Ld2 == 0) = 0; imshow(bw3)

That's it! Read my newsletter article for other thoughts on image segmentation using the watershed transformation.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.