MATLAB image display – grayscale and binary images
In my previous posts (February 9, February 22, and February 29), I discussed the truecolor and indexed image display models in MATLAB, as well as the direct and scaled variations of indexed display. The Image Processing Toolbox has conventions for two additional image display models: grayscale and binary. These conventions are used by the MATLAB image display function imshow, which originated in the Image Processing Toolbox.
Contents
Grayscale image display
If you pass a single argument to imshow, it interprets the input as a grayscale image. Here's an illustration using a simple sinusoid:
theta = linspace(0, 2*pi, 256); I = repmat((-cos(2*theta) + 1)/2, [256 1]); im = imshow(I);
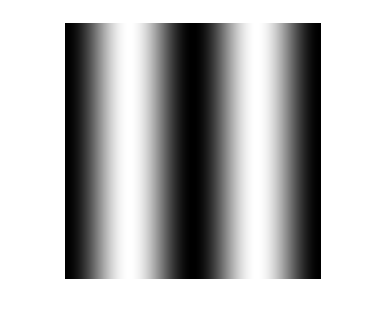
As far as the MATLAB Graphics system is concerned, this is a scaled indexed image being displayed in a figure with a grayscale colormap installed. Here are the key properties that have been set to control the image display:
ax = gca; fig = gcf; im.CDataMapping
ans = scaled
ax.CLim
ans =
0 1
map = fig.Colormap; map(1:5,:)
ans =
0 0 0
0.0039 0.0039 0.0039
0.0078 0.0078 0.0078
0.0118 0.0118 0.0118
0.0157 0.0157 0.0157
The function imshow handles all these details for you.
Controlling the grayscale display range
Using imshow, you can override the conventional display range and specify your own black and white values. You do this by providing a second input argument, a two-element vector containing the black and white values. In the call to imshow below, 0.4 (and any lower value) gets displayed as black. The value 0.6 (and any higher value) gets displayed as white.
imshow(I, [0.4 0.6])
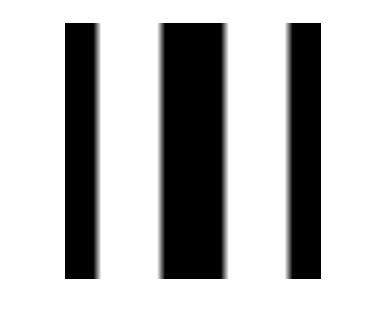
Binary image display
The other Image Processing Toolbox image display model is the binary image. If you supply a single input argument that is logical, then imshow (as well as many other toolbox functions) interpret that input as a binary image.
bw = imread('text.png');
islogical(bw)
ans =
1
imshow(bw)

- Category:
- Pixel colors
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.