Variations on Connected Objects – Using imfill
Reader Uri Pe'er found an old post from 2011 about shortest paths in binary images, and he asked this follow-up question (paraphrased):
How can I determine if there is a path from one row to another in a binary image? And can I constrain the direction of movement along the path?
That sounds fun. Let's give it a try.
I can think of several different approaches. Today I'm going to tackle it using imfill.
Here's a sample image I just drew up.
bw1 = imread('https://blogs.mathworks.com/steve/files/path-shapes-1.png');
imshow(bw1)
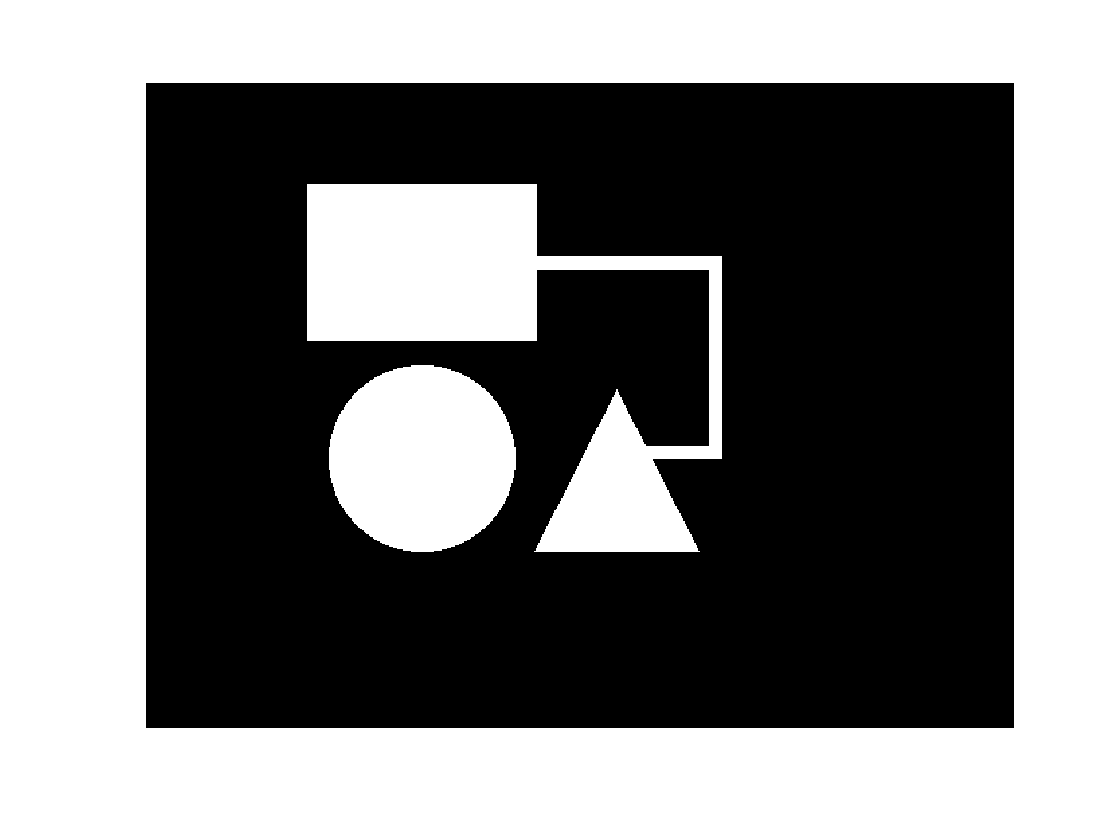
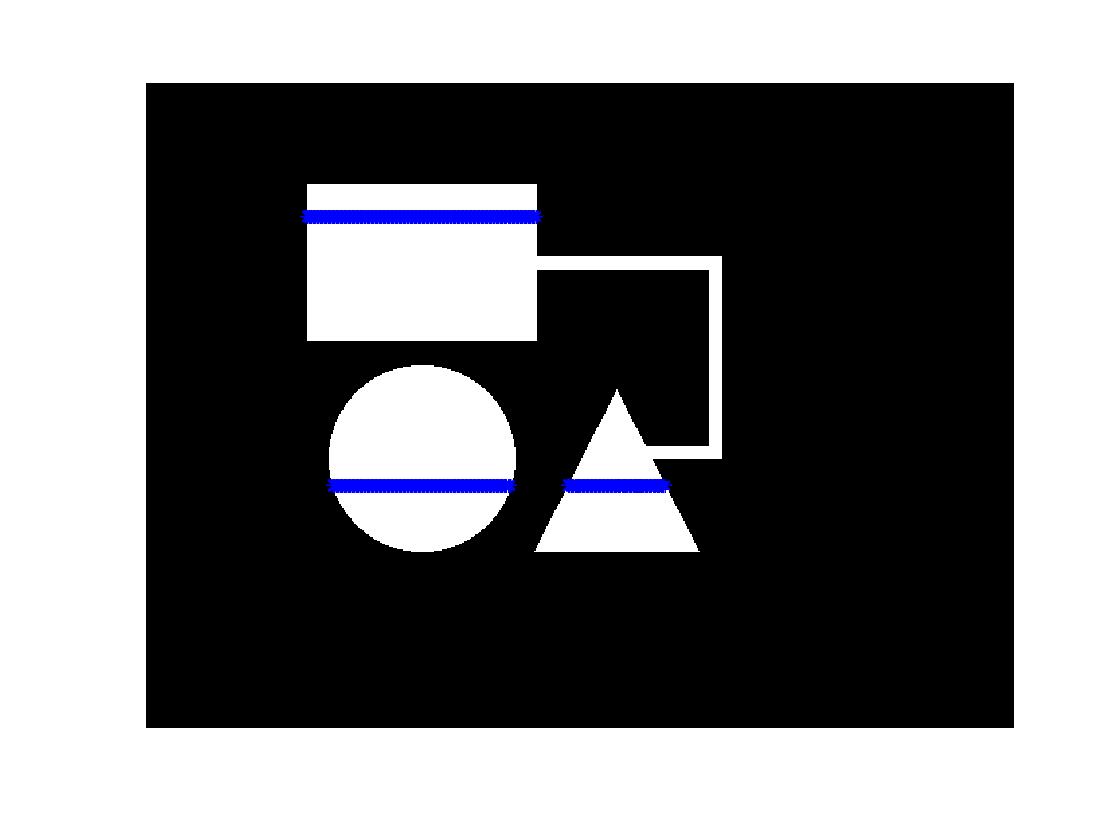
Let's use imfill to see if there is a path from any of the foreground pixels on row 100 to any of the foreground pixels on row 300. First, find the foreground pixels on those rows.
fg_cols_row_100 = find(bw1(100,:)); fg_cols_row_300 = find(bw1(300,:)); hold on plot(fg_cols_row_100,100,'b*') plot(fg_cols_row_300,300,'b*') hold off
Now let's perform an imfill operation starting from all the foreground pixels on row 100. Because imfill fills in background pixels, we need to complement the image first.
bw1a = ~bw1;
imshow(bw1a)
title('Complemented image')

Now perform the fill in the complemented image.
seed_pixels = [100*ones(numel(fg_cols_row_100),1) fg_cols_row_100'];
bw1b = imfill(bw1a,seed_pixels);
imshow(bw1b)
title('Filled image')

Which pixels changed as a result of the fill?
bw1c = bw1b & ~bw1a;
imshow(bw1c)
title('Pixels changed by the fill operation')

If there are any foreground pixels on row 300 of bw1c, then that means row 100 is connected to row 300.
connected = any(bw1c(300,:))
connected = logical 1
Let's try the steps above on another image.
bw2 = imread('https://blogs.mathworks.com/steve/files/path-shapes-2.png'); imshow(bw2) title('Image 2')

fg_cols_row_100 = find(bw1(100,:)); fg_cols_row_300 = find(bw1(300,:)); bw2a = ~bw2; seed_pixels = [100*ones(numel(fg_cols_row_100),1) fg_cols_row_100']; bw2b = imfill(bw2a,seed_pixels); bw2c = bw2b & ~bw2a; connected = any(bw2c(300,:))
connected = logical 0
So we have computed that there is no path connecting rows 100 and 300 in the second image.
OK, what about the second part of Uri's question? How do we constrain the path? For example, how do we constrain the problem to allow movement from the upper-left-to-lower-right diagonal?
We can do that by specifying a custom connectivity when we call imfill. Here's another sample image to test the concept.
bw3 = imread('https://blogs.mathworks.com/steve/files/path-shapes-3.png'); imshow(bw3) fg_cols_row_100 = find(bw3(100,:)); fg_cols_row_300 = find(bw3(300,:)); hold on plot(fg_cols_row_100,100,'b*') plot(fg_cols_row_300,300,'b*') hold off
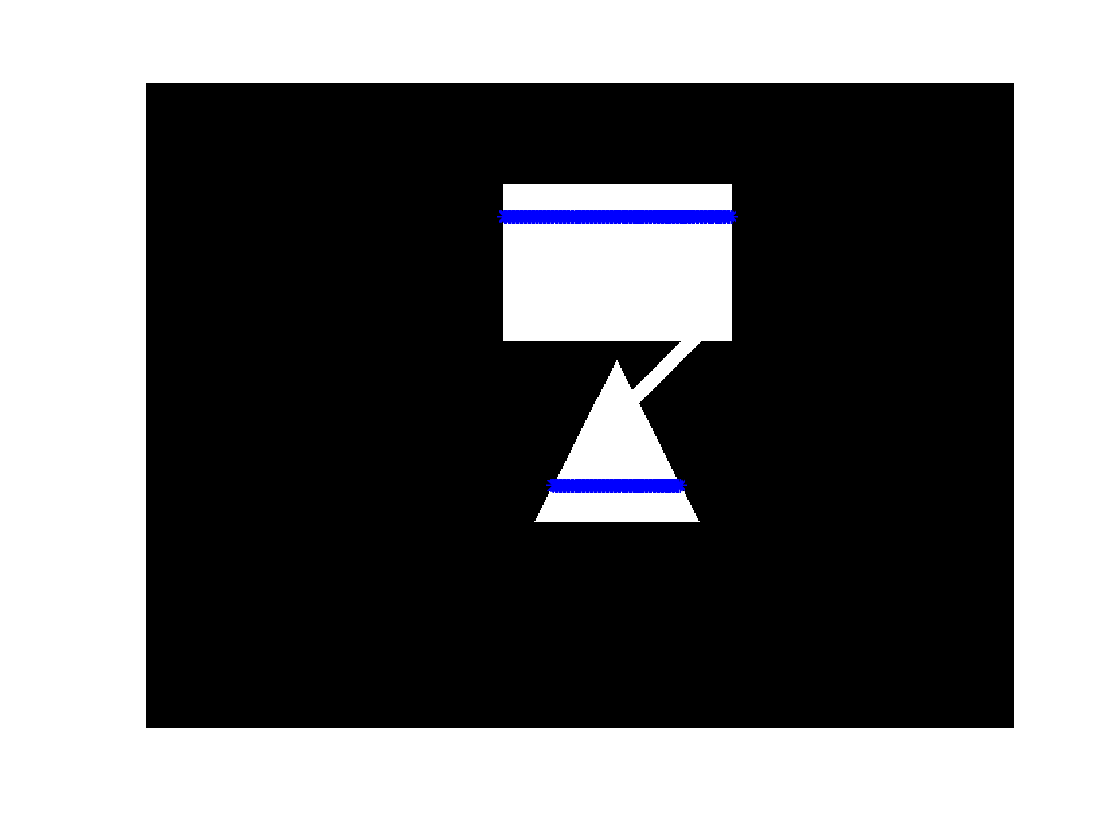
You can specify a custom connectivity using a 3x3 matrix. Here is one that only allows movement along the upper-left-to-lower-right diagonal.
conn = [
1 0 0
0 1 0
0 0 1 ];
Now use that connectivity matrix with imfill.
bw3a = ~bw3; seed_pixels = [100*ones(numel(fg_cols_row_100),1) fg_cols_row_100']; bw3b = imfill(bw3a,seed_pixels,conn); bw3c = bw3b & ~bw3a; imshow(bw3c)

The odd-looking shape above is the set of pixels reachable from foreground pixels on row 100 traveling only along the specified diagonal. With this constrained path, rows 100 and 300 are not connected.
connected = any(bw3c(300,:))
connected = logical 0
But what if we use the opposite diagonal for our path constraint?
conn = [
0 0 1
0 1 0
1 0 0 ];
bw3b = imfill(bw3a,seed_pixels,conn);
bw3c = bw3b & ~bw3a;
imshow(bw3c)

You can see that rows 100 and 300 are still not connected. Let's try rows 180 and 250.
imshow(bw3) fg_cols_row_180 = find(bw3(180,:)); fg_cols_row_250 = find(bw3(250,:)); hold on plot(fg_cols_row_180,180,'b*') plot(fg_cols_row_250,250,'b*') hold off

seed_pixels = [180*ones(numel(fg_cols_row_180),1) fg_cols_row_180']; bw3b = imfill(bw3a,seed_pixels,conn); bw3c = bw3b & ~bw3a; imshow(bw3c)

And rows 180 and 250 are connected.
connected = any(bw3c(250,:))
connected = logical 1
Next time I plan to take another look at this problem using MATLAB graph operations.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.