How to Compute Perceptual Color Difference
I wrote previously about the new colorChecker, which can detect X-Rite test charts in the R2020b release. Another area of new color-related functionality is computing perceptual color differences. There is the new function deltaE, which computes color differences based on the L*a*b* color space and the CIE76 standard. There is also the imcolordiff function, which can compute color differences based either on the CIE94 or the CIEDE2000 standard.
I recently mentioned to someone on the Image Processing Toolbox team that I was planning to write a blog post about these functions, and he posed the following question: which two colors are the furthest apart, perceptually speaking? I decided to give that a try using $\Delta_E$. I'll formulate the problem this way: which two sRGB colors have the largest $\Delta_E$ between them?
In a related post back in 2015, I demonstrated how to plot the sRGB gamut surface in L*a*b* space, like this:
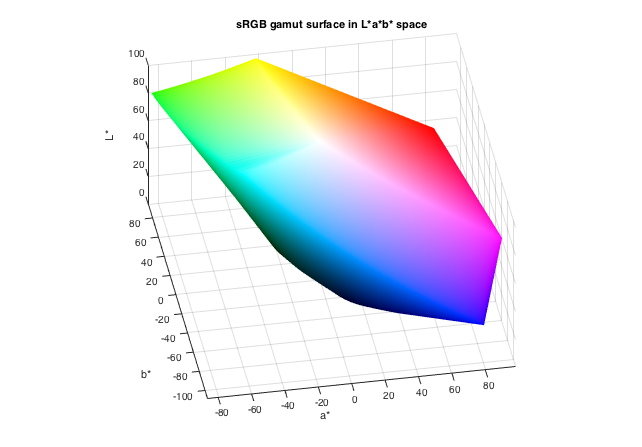
Looking at this diagram, you might be able to guess the answer. But, let's work through it. The first thing I want to do is to sample the sRGB space.
[r,g,b] = ndgrid(linspace(0,1,100)); rgb = [r(:), g(:), b(:)];
Next, convert the sRGB colors to Lab. (I'm going to stop typing the "*" characters.)
lab = rgb2lab(rgb);
Now let's find the colors on the convex hull of the Lab values. The pair of colors most distant from each other must both be on the convex hull.
k = convhull(lab); hull_colors = lab(unique(k(:,1)),:);
If this were a two-dimensional problem, then I know of an algorithm that can find the most distant pair of points in $O(N)$, where $N$ is the number of points on the convex hull. I don't know of a similar algorithm in three dimensions, so I'm just going to brute force it by computing the distance between every color pair.
So, how many colors are we talking about?
size(hull_colors)
ans =
3980 3
There are 3908 colors, each of which is represented by a 3-element vector in Lab space. The color difference $\Delta_E$ is the Euclidean distance between two colors in Lab space. I want to compute the distance between every color in that set and every other color. Here is a nifty and compact way to do that using the implicit expansion behavior of MATLAB arithmetic operators.
C1 = reshape(hull_colors,[],1,3); C2 = reshape(hull_colors,1,[],3); Cdiff = C1 - C2; DE = sqrt(sum(Cdiff.^2,3)); size(DE)
ans =
3980 3980
You can see that DE is an 3980x3980 matrix. It contains the pair-wise distances between all the convex hull colors. (See also pdist2, a function in the Statistics and Machine Learning Toolbox that can compute pair-wise vector distances with much more flexibility, as well as hypot, a MATLAB function that computes the magnitude of a two-element vector in a way that avoids numerical overflow and underflow problems.)
Let's find where the maximum distances are in this matrix.
[m,n] = find(DE == max(DE(:)))
m =
3883
92
n =
92
3883
What are those colors (in Lab space)?
max_colors_lab = hull_colors(m,:)
max_colors_lab = 32.2970 79.1875 -107.8602 87.7347 -86.1827 83.1793
And those two colors in sRGB space:
max_colors_rgb = lab2rgb(max_colors_lab)
max_colors_rgb =
0.0000 -0.0000 1.0000
0.0000 1.0000 0.0000
They are just the sRGB green and blue primaries.
colorSwatches(max_colors_rgb) axis equal axis off

(colorSwatches is a DIPUM3E function that is available to you in MATLAB Color Tools on the File Exchange and on GitHub.)
These two colors have a $\Delta_E$ of:
DE(m(1),n(1))
ans = 258.6827
The deltaE function offers a more convenient way to compute $\Delta_E$:
deltaE([0 1 0],[0 0 1])
ans = 258.6827
Some other time, I will write about the other color difference calculations provided by imcolordiff.









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.